
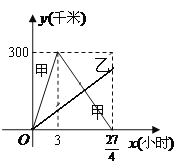
����Ŀ����֪���ס��������ֱ�����300ǧ�� A,B����ͬʱ����������У����м� B�غ��������أ���ͼ����������Գ����صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ���ͼ����
��1����׳�������صľ��� y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��2����������ʻ������Գ����صľ������ʱ������ ![]() Сʱ�����ҳ�������صľ��� y��ǧ�ף�����ʻʱ�� x��Сʱ��֮��ĺ�����ϵʽ��
Сʱ�����ҳ�������صľ��� y��ǧ�ף�����ʻʱ�� x��Сʱ��֮��ĺ�����ϵʽ��
��3���ڣ�2���������£�����������ʻ�Ĺ�����������ʱ�䣮
���𰸡�������
��������������
��1����ͼ֪���ú�����ϵ�ڲ�ͬ��ʱ������ֳɲ�ͬ�Ĺ�ϵ����ֶα������ʻʱ��С��3ʱ������������������ʹʱ�����3С��![]() ʱ��һ�κ������ɸ��ݴ���ϵ�����з��̣�������ϵʽ��
ʱ��һ�κ������ɸ��ݴ���ϵ�����з��̣�������ϵʽ��
��2��4.5Сʱ����3������һ�κ�����ϵʽ��������ҳ�������![]() Сʱ��ʹ�ľ��룮��ͼ��ɿ������ҳ�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮����������������ϵ���ô���ϵ��������⣮
Сʱ��ʹ�ľ��룮��ͼ��ɿ������ҳ�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮����������������ϵ���ô���ϵ��������⣮
��3������������У�����ʱ�ס���������ʹ�ľ���֮��Ϊ300ǧ�ף��г����̽��������������������
��⣺
��1����1����0��x��3ʱ������������������Ϊy=kx��
x=3ʱ��y=300��������k=100������y=100x��
��3��x��![]() ʱ����һ�κ�������Ϊy=kx+b��
ʱ����һ�κ�������Ϊy=kx+b��
�������㣨3��300������![]() ��0������
��0������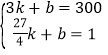
���![]() ��
��
����y=540��80x��
�ۺ����ϵü׳�������صľ���y����ʻʱ��x֮��ĺ�����ϵʽ Ϊ��y=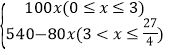 ��
��
��2����x=![]() ʱ��y��=540��80��
ʱ��y��=540��80��![]() =180��
=180��
�ҳ����㣨![]() ��180����y��=40x����0��x��
��180����y��=40x����0��x��![]() ��
��
��3��������������������
�ٵ�0��x��3��100x+40x=300�����x=![]() ��
��
�ڵ�3��x��![]() ʱ����540��80x��+40x=300�����x=6��
ʱ����540��80x��+40x=300�����x=6��
����������������һ������ʱ��Ϊ��![]() Сʱ���ڶ�������ʱ��Ϊ��6Сʱ��
Сʱ���ڶ�������ʱ��Ϊ��6Сʱ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c����![]()
��1����a��b��c��ֵ��
��2��������a��b��cΪ���ܷ������Σ����ܹ��������Σ���������ε��ܳ��������ܹ��������Σ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
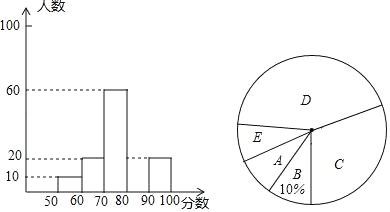
����Ŀ��2018����ʱ������쿪�ݺ�������������������ǰһ�ܣ�ijУ���꼶��ѧ�о�ѧϰС����ijʮ��·��������鲿������ԡ����������������˽������ͳ�ƽ�����������ͼ��������������ͳ��ͼ������ͼ��������ݻش��������⣺
A | 50��n��60 |
B | 60��n��70 |
C | 70��n��80 |
D | 80��n��90 |
E | 90��n��100 |
��1�����ε����������Ϊ�� ���ˣ�������ͳ��ͼ�С�C���������ε�Բ�ĽǵĶ���Ϊ�� ���ȣ�
��2����ȫƵ���ֲ�ͼ��
��3��������һ�����·�ڹ���7000��ͨ��������Ƶ÷ֳ���80�Ĵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ��a��b������һ��������![]() ��Ϊ��ab=a2 +ab��2�����������⣺
��Ϊ��ab=a2 +ab��2�����������⣺
��1![]() 3=2��
3=2��
�ڷ���x![]() 1=0�ĸ�Ϊ��x1 =��2��x2 =1��
1=0�ĸ�Ϊ��x1 =��2��x2 =1��
�۲���ʽ�� ![]() �Ľ⼯Ϊ����1��x��4��
�Ľ⼯Ϊ����1��x��4��
�ܵ㣨![]() ��
��![]() ���ں���y=x
���ں���y=x![]() ����1����ͼ���ϣ�
����1����ͼ���ϣ�
������ȷ���ǣ� ��
A. �٢ڢۢ� B. �٢� C. �٢ڢ� D. �ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӣ�1��1��2�����������У������ȡһ������Ϊa����ô��ʹ����x��һ�κ���y��2x��a��ͼ����x�ᡢy��Χ�ɵ������ε����Ϊ![]() ����ʹ����x�IJ���ʽ��
����ʹ����x�IJ���ʽ��![]() �н�ĸ���Ϊ________��
�н�ĸ���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
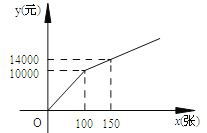
����Ŀ���ڹ���ij����������Ʊʱ���蹺����Ʊ��Ϊx���ţ����ܷ���Ϊy��Ԫ�����������ֹ�����
����һ������λ��������10000Ԫ����õ�λ������Ʊ�ļ۸�Ϊÿ��60Ԫ��
���ܷ��ã����������+��Ʊ�ѣ�
��������������Ʊ��ʽ��ͼ��ʾ��
����������⣺
��1������һ�У�y��x�ĺ�����ϵʽΪ ��
�������У���0��x��100ʱ��y��x�ĺ�����ϵʽΪ ��
��x��100ʱ��y��x�ĺ�����ϵʽΪ ��
��2�����������������Ʊ����100�ţ��㽫ѡ����һ�ַ�����ʹ�ܷ�����ʡ����˵�����ɣ�
��3���ס�������λ�ֱ���÷���һ��������������������Ʊ��700�ţ���ȥ�ܷ��ü�58000Ԫ����ס�������λ��������Ʊ�����ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
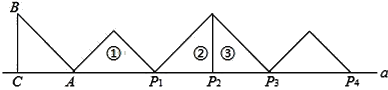
����Ŀ����ͼ������Rt��ABC�У���ACB=90�㣬AC=BC=1����AC����ֱ��a�ϣ�����ABC�Ƶ�A˳ʱ����ת��λ�����ɵõ���P1����ʱAP1=![]() ����λ�������������Ƶ�P1˳ʱ����ת��λ�����ɵõ���P2����ʱAP2=
����λ�������������Ƶ�P1˳ʱ����ת��λ�����ɵõ���P2����ʱAP2=![]() +1����λ�������������Ƶ�P2˳ʱ����ת��λ�����ɵõ���P3ʱ��AP3=
+1����λ�������������Ƶ�P2˳ʱ����ת��λ�����ɵõ���P3ʱ��AP3=![]() +2�����˹��ɼ�����ת��ֱ���õ���
+2�����˹��ɼ�����ת��ֱ���õ���![]() Ϊֹ����
Ϊֹ����![]() =________��
=________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����ֱ��x=m��˫����yn=![]() �Ľ���Am �� n��m��nΪ��������Ϊ��˫����㡱��˫����yn=
�Ľ���Am �� n��m��nΪ��������Ϊ��˫����㡱��˫����yn=![]() �ڵ�һ�����ڵIJ���������ֱ����ƽ�ƻ���ƽ����x���ֱ��Ϊ�Գ�����з���֮��õ��ĺ���ͼ��Ϊ�䡰�������ߡ���
�ڵ�һ�����ڵIJ���������ֱ����ƽ�ƻ���ƽ����x���ֱ��Ϊ�Գ�����з���֮��õ��ĺ���ͼ��Ϊ�䡰�������ߡ���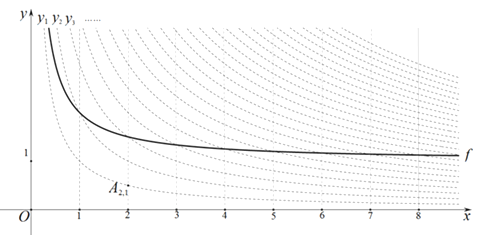
��1���١�˫����㡱A2 �� 1������Ϊ �������߶�A4 �� 3A4 �� n�ij�Ϊ1����λ���ȣ���n= ��
��2��ͼ�е�����f��˫����y1=![]() ��һ�����������ߡ����Ҿ�����A2 �� 3 �� ��f�Ľ���ʽΪy=
��һ�����������ߡ����Ҿ�����A2 �� 3 �� ��f�Ľ���ʽΪy=
��3������˫����y3=![]() �ġ��������ߡ�g��g��˫����y3=
�ġ��������ߡ�g��g��˫����y3=![]() ���غϣ���ʹ�侭����˫����㡱A2 �� a��A3 �� 3��A4 �� b ��
���غϣ���ʹ�侭����˫����㡱A2 �� a��A3 �� 3��A4 �� b ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AB��3��BC��2����AC��AD�ҡ�ACD��60�㣬��Խ���BD�ij����ֵΪ______________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com