
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����ֱ��x=m��˫����yn=![]() �Ľ���Am �� n��m��nΪ��������Ϊ��˫����㡱��˫����yn=
�Ľ���Am �� n��m��nΪ��������Ϊ��˫����㡱��˫����yn=![]() �ڵ�һ�����ڵIJ���������ֱ����ƽ�ƻ���ƽ����x���ֱ��Ϊ�Գ�����з���֮��õ��ĺ���ͼ��Ϊ�䡰�������ߡ���
�ڵ�һ�����ڵIJ���������ֱ����ƽ�ƻ���ƽ����x���ֱ��Ϊ�Գ�����з���֮��õ��ĺ���ͼ��Ϊ�䡰�������ߡ���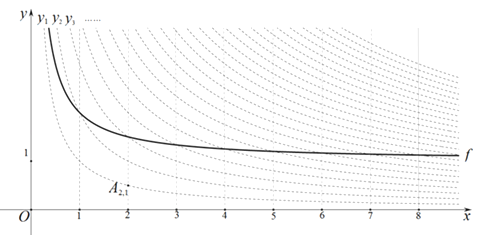
��1���١�˫����㡱A2 �� 1������Ϊ �������߶�A4 �� 3A4 �� n�ij�Ϊ1����λ���ȣ���n= ��
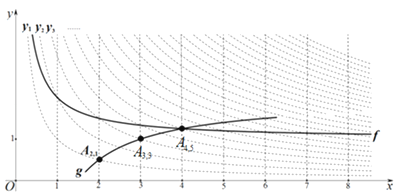
��2��ͼ�е�����f��˫����y1=![]() ��һ�����������ߡ����Ҿ�����A2 �� 3 �� ��f�Ľ���ʽΪy=
��һ�����������ߡ����Ҿ�����A2 �� 3 �� ��f�Ľ���ʽΪy=
��3������˫����y3=![]() �ġ��������ߡ�g��g��˫����y3=
�ġ��������ߡ�g��g��˫����y3=![]() ���غϣ���ʹ�侭����˫����㡱A2 �� a��A3 �� 3��A4 �� b ��
���غϣ���ʹ�侭����˫����㡱A2 �� a��A3 �� 3��A4 �� b ��
���𰸡�
��1����2��![]() ����7
����7
��2��y=![]()
��3��
�⣺��x=2����y=![]() ��y=
��y=![]() ����A2��a�������ǣ�2��
����A2��a�������ǣ�2��![]() ����
����
��x=3����y=![]() ��y=1����A3��3�������ǣ�3��1����
��y=1����A3��3�������ǣ�3��1����
��x=4����y=![]() ��y=
��y=![]() ����A4��b�������ǣ�4��
����A4��b�������ǣ�4��![]() ����
����
��ͼ��
����������1���ٰ�x=2����y=![]() ������õ�������ꣻ
������õ�������ꣻ
���������A4 �� 3A4 �� n�����꣬Ȼ������߶�A4 �� 3A4 �� n�ij�Ϊ1����λ���ȼ������n��ֵ��
��2����x=2����y=![]() ��õ�A2 �� 3�����꣬Ȼ����f�Ľ���ʽΪy=
��õ�A2 �� 3�����꣬Ȼ����f�Ľ���ʽΪy=![]() +k���ѵ�A2 �� 3��������뼴�����k��ֵ��������ô���ʽ��
+k���ѵ�A2 �� 3��������뼴�����k��ֵ��������ô���ʽ��
��3��������á�˫����㡱A2 �� a��A3 �� 3��A4 �� b�����꣬��y=![]() ��������ƽ�ƻ��y=
��������ƽ�ƻ��y=![]() ��ƽ����x���ֱ�߷��ۣ�����ƽ�Ƽ�����ã�
��ƽ����x���ֱ�߷��ۣ�����ƽ�Ƽ�����ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���ABCD�У��ֱ���AD��BCΪ���������ȱ���ADE�͵ȱ���BCF������BE��DF����֤���ı���BEDF��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
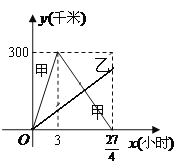
����Ŀ����֪���ס��������ֱ�����300ǧ�� A,B����ͬʱ����������У����м� B�غ��������أ���ͼ����������Գ����صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ���ͼ����
��1����׳�������صľ��� y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��2����������ʻ������Գ����صľ������ʱ������ ![]() Сʱ�����ҳ�������صľ��� y��ǧ�ף�����ʻʱ�� x��Сʱ��֮��ĺ�����ϵʽ��
Сʱ�����ҳ�������صľ��� y��ǧ�ף�����ʻʱ�� x��Сʱ��֮��ĺ�����ϵʽ��
��3���ڣ�2���������£�����������ʻ�Ĺ�����������ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C��D��Բ�ϵ����㣮��BC=8��cosD=![]() �� ��AB�ij�Ϊ��������
�� ��AB�ij���������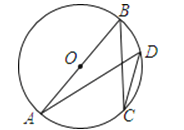
A.![]()
B.![]()
C.![]()
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�˫����y=![]() ��ֱ��y=kx��2���ڵ�A��3��1����
��ֱ��y=kx��2���ڵ�A��3��1����
��1����ֱ�ߺ�˫���ߵĽ���ʽ��
��2��ֱ��y=kx��2��x�ύ�ڵ�B����P��˫����y=![]() ��һ�㣬����P��ֱ��PC��x�ᣬ��y���ڵ�C����ֱ��y=kx��2�ڵ�D����DC=2OB��д����P������.
��һ�㣬����P��ֱ��PC��x�ᣬ��y���ڵ�C����ֱ��y=kx��2�ڵ�D����DC=2OB��д����P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC����DCB������һ��������ʹ��ABC�ա�DCB�������ӵ�������_____����ע��ֻ��д��һ���������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ũ�����������У���һ����¥��Ҫ�������ۣ�ij¥�̹�23�㣬���ۼ۸����£��ڰ˲�¥���ۼ�Ϊ4000Ԫ/��2���ӵڰ˲���ÿ����һ�㣬ÿƽ�����ۼ����50Ԫ����֮��¥��ÿ�½�һ�㣬ÿƽ�����ۼ۽���30Ԫ����֪��¥��ÿ��¥�������Ϊ120��2��
��������һ���Ը������з���������������Żݷ�����
����һ������8%������ÿ��¥������aԪװ����
������������10%��û���������ͣ�
��1����д���ۼ�y��Ԫ/��2����¥��x��1��x��23��xȡ������֮��ĺ�����ϵʽ��
��2������Ҫ�����ʮ�����һ��¥��������һ���Ը��幺�����������������Żݷ������Ӻ��㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һ��ƽ����l1��l2��l3��l4��������ABCD���ĸ�����ֱ���l1��l2��l3��l4�ϣ�EG����D�Ҵ�ֱl1�ڵ�E���ֱ�l2��l4�ڵ�F��G��EF=DG=1��DF=2��
��1��AE=__________��������ABCD�ı߳�=__________��
��2����ͼ2������AEG�Ƶ�A˳ʱ����ת�õ���AE��D�䣬��ת��Ϊ����0�㣼����90�㣩����D����ֱ��l3�ϣ���AD��Ϊ����E��D�����������AB��C��D�䣬ʹB�䡢C��ֱ���ֱ��l2��l4�ϣ�
��д����B��AD�������������ϵ������֤����
������=30�㣬ֱ��д������AB��C��D��ı߳�Ϊ__________��
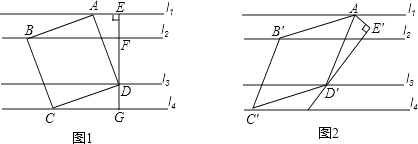
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ�����Ŀڴ���ԭ��װ��1������2������ÿ�������ɫ����ȫ��ͬ�������н������������İ취�У�ʹ�ý���ҡ�ȣ�������������һ����������������������ĸ��ʲ����Ϊ�� ��
A. �ڴ��з���1������ B. �ڴ��з���1������2������
C. �ڴ���ȡ��1������ D. �ڴ��з���2������1������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com