
【题目】如图1,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点分别在l1,l2,l3,l4上,EG过点D且垂直l1于点E,分别交l2,l4于点F,G,EF=DG=1,DF=2.
(1)AE=__________,正方形ABCD的边长=__________;
(2)如图2,将∠AEG绕点A顺时针旋转得到∠AE′D′,旋转角为α(0°<α<90°),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′、C′分别在直线l2,l4上.
①写出∠B′AD′与α的数量关系并给出证明;
②若α=30°,直接写出菱形AB′C′D′的边长为__________.
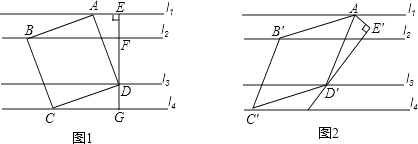
【答案】(1)1;![]() (2)①∠B'AD'=90°-α;(3)
(2)①∠B'AD'=90°-α;(3)![]()
【解析】分析:
(1)如下图1,由图结合已知条件可证得△AED≌△DGC,由此即可得到AE=DG=1;
(2)①如下图2,过点B′作B′M垂直于l1于点M,通过证Rt△AED′≌Rt△B′MA可得∠D′AE+∠B′AM=90°,由此可得∠B′AD′+α=90°,即∠B′AD′=90°-α;
②如下图2,由l1∥l2∥l3可过点E′作E′O⊥l1于点O,E′O⊥l3于点N,当α=30°时,易得OE=![]() AE=
AE=![]() ,∠D′EN=30°,结合ON=3可得EN=
,∠D′EN=30°,结合ON=3可得EN=![]() ,由此易得D′E=
,由此易得D′E=![]() ,这样在Rt△AD′E中即可由勾股定理求得AD′的长.
,这样在Rt△AD′E中即可由勾股定理求得AD′的长.
详解:
(1)如下图1,由题意可得∠AEF=∠ADC=∠CGD=90°,
∴∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
又∵AD=CD,
∴△AED≌△DGC,
∴AE=DG=1,
又∵DE=EF+FD=1+2=3,
∴AD=![]() ,即正方形ABCD的边长为
,即正方形ABCD的边长为![]() ;
;
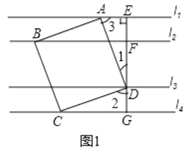
(2)①∠B′AD′=90°-α;理由如下:
如下图2,过点B′作B′M垂直于l1于点M,
∴∠B′MA=∠D′EA=90°,
由(1)可知MB′=AE=1,又∵AB′=ED′,
∴Rt△AED′≌Rt△B′MA,
∴∠B′AM=∠AD′E,
又∵∠D′AE+∠AD′E=90°,
∴∠D′AE+∠B′AM=90°,
∴∠B′AD′+α=90°,即∠B′AD′=90°-α;
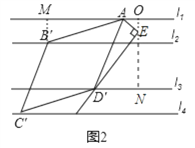
(3)如上图2,由由l1∥l2∥l3可过点E′作E′O⊥l1于点O,E′O⊥l3于点N,
∵α=30°,
∴OE==![]() AE=
AE=![]() ,∠D′EN=30°,
,∠D′EN=30°,
又∵ON=3,
∴EN=![]() ,
,
∴在Rt△D′EN中,D′E=![]() ,
,
∴在Rt△AD′E中,AD′=![]() ,
,
即菱形AB′C′D′的边长为![]() .
.


科目:初中数学 来源: 题型:
【题目】对于实数a、b,定义一种运算“![]() ”为:ab=a2 +ab-2,有下列命题:
”为:ab=a2 +ab-2,有下列命题:
①1![]() 3=2;
3=2;
②方程x![]() 1=0的根为:x1 =-2,x2 =1;
1=0的根为:x1 =-2,x2 =1;
③不等式组 ![]() 的解集为:-1<x<4;
的解集为:-1<x<4;
④点(![]() ,
,![]() )在函数y=x
)在函数y=x![]() (-1)的图象上.
(-1)的图象上.
其中正确的是( )
A. ①②③④ B. ①③ C. ①②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,定义直线x=m与双曲线yn=![]() 的交点Am , n(m、n为正整数)为“双曲格点”,双曲线yn=
的交点Am , n(m、n为正整数)为“双曲格点”,双曲线yn=![]() 在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.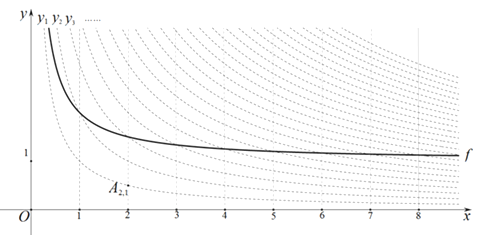
(1)①“双曲格点”A2 , 1的坐标为 ;②若线段A4 , 3A4 , n的长为1个单位长度,则n= ;
(2)图中的曲线f是双曲线y1=![]() 的一条“派生曲线”,且经过点A2 , 3 , 则f的解析式为y=
的一条“派生曲线”,且经过点A2 , 3 , 则f的解析式为y=
(3)画出双曲线y3=![]() 的“派生曲线”g(g与双曲线y3=
的“派生曲线”g(g与双曲线y3=![]() 不重合),使其经过“双曲格点”A2 , a、A3 , 3、A4 , b .
不重合),使其经过“双曲格点”A2 , a、A3 , 3、A4 , b .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上任一点,AB=12 cm,C、D两点分别从P、B同时向A点运动,且C点的运动速度为2 cm/s,D点的运动速度为3 cm/s,运动的时间为t s.
![]()
(1)若AP=8 cm.
①运动1 s后,求CD的长;
②当D在线段PB运动上时,试说明AC=2CD;
(2)如果t=2 s时,CD=1 cm,试探索AP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是按一定规律排列且形式相似的一列数:
第1个数:a1=![]() -(1+
-(1+![]() );
);
第2个数:a2=![]() -(1+
-(1+![]() )[1+
)[1+![]() ][1+
][1+![]() ];
];
第3个数:a3=![]() -(1+
-(1+![]() )[1+
)[1+![]() ][1+
][1+![]() ][1+
][1+![]() ](1+
](1+![]() ].
].
(1)计算这三个数的结果(直接写答案):
a1=___;a2=___;a3=___;
(2)请按上述规律写出第4个数a4的形式并计算结果;
(3)请根据上述规律写出第n (n为正整数)个数an的形式(中间部分用省略号,两端部分必须写详细),然后直接写出计算结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.
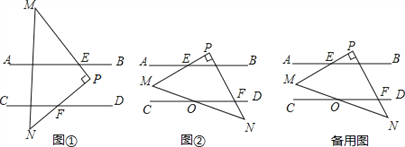
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应学校提出的“节能减排,低碳生活”的倡议,班会课上小李建议每位同学都践行“双面打印,节约用纸”.他举了一个实际例子:打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,总质量为160克.已知每页薄型纸比厚型纸轻0.8克,求例子中的A4厚型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨9 000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量比第一次的2倍还多300 kg.如果超市按9元/kg的价格出售,当大部分干果售出后,余下的600 kg按售价的八折售完.
(1)该种干果第一次的进价是多少?
(2)超市销售这种干果共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com