
【题目】如图,P是线段AB上任一点,AB=12 cm,C、D两点分别从P、B同时向A点运动,且C点的运动速度为2 cm/s,D点的运动速度为3 cm/s,运动的时间为t s.
![]()
(1)若AP=8 cm.
①运动1 s后,求CD的长;
②当D在线段PB运动上时,试说明AC=2CD;
(2)如果t=2 s时,CD=1 cm,试探索AP的值.
【答案】(1)3cm,(2)见解析;(3)9 cm或11 cm.
【解析】(1)①先求出PB、CP与DB的长度,然后利用CD=CP+PB-DB即可求出答案.②用t表示出AC、DP、CD的长度即可求证AC=2CD;
(2)当t=2时,求出CP、DB的长度,由于没有说明D点在C点的左边还是右边,故需要分情况讨论.
试题解析:(1)①由题意可知:CP=2×1=2(cm),DB=3×1=3(cm).
因为AP=8 cm,AB=12 cm,
所以PB=AB-AP=4 cm.
所以CD=CP+PB-DB=2+4-3=3(cm).
②因为AP=8 cm,AB=12 cm,
所以BP=4 cm,AC=(8-2t)cm.
所以DP=(4-3t)cm.
所以CD=CP+DP=2t+4-3t=(4-t)cm.
所以AC=2CD.
(2)当t=2时,CP=2×2=4(cm),DB=3×2=6(cm),
当点D在点C的右边时,如图所示:
![]()
因为CD=1 cm,
所以CB=CD+DB=7 cm.
所以AC=AB-CB=5 cm.
所以AP=AC+CP=9 cm.
当点D在点C的左边时,如图所示:
![]()
所以AD=AB-DB=6 cm.
所以AP=AD+CD+CP=11 cm.
综上所述,AP=9 cm或11 cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为100° 的菱形,剪口与折痕所成的角的度数应为( )
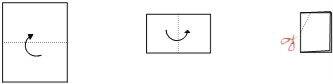
A. 25°或50° B. 20°或50° C. 40°或50° D. 40°或80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别.
(1)随机从箱子里取出1个球,则取出黄球的概率是多少?
(2)随机从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法表示出所有可能出现的结果,并求两次取出的都是白色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点分别在l1,l2,l3,l4上,EG过点D且垂直l1于点E,分别交l2,l4于点F,G,EF=DG=1,DF=2.
(1)AE=__________,正方形ABCD的边长=__________;
(2)如图2,将∠AEG绕点A顺时针旋转得到∠AE′D′,旋转角为α(0°<α<90°),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′、C′分别在直线l2,l4上.
①写出∠B′AD′与α的数量关系并给出证明;
②若α=30°,直接写出菱形AB′C′D′的边长为__________.
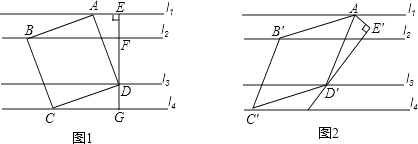
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正方体,六个面上分别写有六个连续的整数(如图所示),且每两个相对面上的数字和相等,本图所能看到的三个面所写的数字分别是:![]() ,
,![]() ,
,![]() ,问:与它们相对的三个面的数字各是多少?为什么?
,问:与它们相对的三个面的数字各是多少?为什么?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.




(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段_______,_________;S矩形AEFG:S□ABCD=__________.
(2)□ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长;
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出AD、BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com