
【题目】如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.




(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段_______,_________;S矩形AEFG:S□ABCD=__________.
(2)□ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长;
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出AD、BC的长.
【答案】 AE GF 1:2
【解析】分析:(1)由图可直接得到第一、二空答案,根据折叠的性质可得△AEH与△ABE面积相等、梯形HFGA与梯形FCDG面积相等,据此不难得到第三空答案;
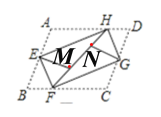
(2)对图形进行点标注,如图所示:首先根据勾股定理求得FH的长,再根据折叠的性质以及请到的知识可得AH=FN,HD=HN,然后根据线段和差关系即可得到AD的长;
(3)根据题目信息,动手这一下,然后将结合画出来,再结合折叠的性质以及勾股定理的知识分析解答即可.
详解:(1)根据题意得:操作形成的折痕分别是线段AE、GF;
由折叠的性质得:△ABE≌△AHE,四边形AHFG≌四边形DCFG,
∴△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,
∴S矩形AEFG=![]() S平行四边形ABCD,
S平行四边形ABCD,
∴S矩形AEFG:S平行四边形ABCD=1:2;
故答案为:AE,GF,1:2;
(2)∵四边形EFGH是矩形,
∴∠HEF=90°,
∴FH=![]() =13,
=13,
由折叠的性质得:AD=FH=13;
由折叠的对称性可知:DH=NH,AH=HM,CF=FN.
易得△AEH≌CGF,
所以CF=AH,
所以AD=DH+AH=HN+FN=FH=13.

(3)有3种折法,如图4、图5、图6所示:
①折法1中,如图4所示:

由折叠的性质得:AD=BG,AE=BE=![]() AB=4,CF=DF=
AB=4,CF=DF=![]() CD=5,GM=CM,∠FMC=90°,
CD=5,GM=CM,∠FMC=90°,
∵四边形EFMB是叠合正方形,
∴BM=FM=4,
∴GM=CM=![]() =3,
=3,
∴AD=BG=BM-GM=1,BC=BM+CM=7;
②折法2中,如图5所示:
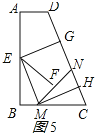
由折叠的性质得:四边形EMHG的面积=![]() 梯形ABCD的面积,AE=BE=
梯形ABCD的面积,AE=BE=![]() AB=4,DG=NG,NH=CH,BM=FM,MN=MC,
AB=4,DG=NG,NH=CH,BM=FM,MN=MC,
∴GH=![]() CD=5,
CD=5,
∵四边形EMHG是叠合正方形,
∴EM=GH=5,正方形EMHG的面积=52=25,
∵∠B=90°,
∴FM=BM=![]() =3,
=3,
设AD=x,则MN=FM+FN=3+x,
∵梯形ABCD的面积=![]() (AD+BC)×8=2×25,
(AD+BC)×8=2×25,
∴AD+BC=![]() ,
,
∴BC=![]() -x,
-x,
∴MC=BC-BM=![]() -x-3,
-x-3,
∵MN=MC,
∴3+x=![]() -x-3,
-x-3,
解得:x=![]() ,
,
∴AD=![]() ,BC=
,BC=![]() -
-![]() =
=![]() ;
;
③折法3中,如图6所示,作GM⊥BC于M,
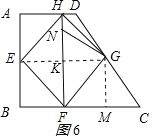
则E、G分别为AB、CD的中点,
则AH=AE=BE=BF=4,CG=![]() CD=5,正方形的边长EF=GF=4
CD=5,正方形的边长EF=GF=4![]() ,
,
GM=FM=4,CM=![]() =3,
=3,
∴BC=BF+FM+CM=11,FN=CF=7,DH=NH=8-7=1,
∴AD=5.


科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上任一点,AB=12 cm,C、D两点分别从P、B同时向A点运动,且C点的运动速度为2 cm/s,D点的运动速度为3 cm/s,运动的时间为t s.
![]()
(1)若AP=8 cm.
①运动1 s后,求CD的长;
②当D在线段PB运动上时,试说明AC=2CD;
(2)如果t=2 s时,CD=1 cm,试探索AP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应学校提出的“节能减排,低碳生活”的倡议,班会课上小李建议每位同学都践行“双面打印,节约用纸”.他举了一个实际例子:打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,总质量为160克.已知每页薄型纸比厚型纸轻0.8克,求例子中的A4厚型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,实线部分为某月牙形公园的轮廓示意图,它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成,⊙P与⊙Q的半径都是2km,点P在⊙Q上.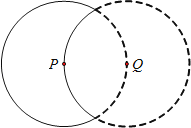
(1)求月牙形公园的面积;
(2)现要在公园内建一块顶点都在⊙P上的直角三角形场地ABC,其中∠C=90°,求场地的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨9 000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量比第一次的2倍还多300 kg.如果超市按9元/kg的价格出售,当大部分干果售出后,余下的600 kg按售价的八折售完.
(1)该种干果第一次的进价是多少?
(2)超市销售这种干果共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=10cm,则AB+BD=cm.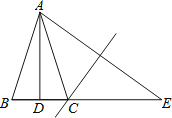
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如下命题:①三角形的中线、角平分线、高都是线段;②三角形的三条高必交于一点;③三角形的三条角平分线必交于一点;④三角形的三条高必在三角形内.其中正确的是( )
A. ①② B. ①③ C. ②④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com