Question

【题目】如图，实线部分为某月牙形公园的轮廓示意图，它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成，⊙P与⊙Q的半径都是2km，点P在⊙Q上．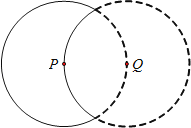

（1）求月牙形公园的面积；
（2）现要在公园内建一块顶点都在⊙P上的直角三角形场地ABC，其中∠C=90°，求场地的最大面积．

Answer 1

【答案】
（1）

解：连接DQ、EQ、PD、PE、PQ、DE．

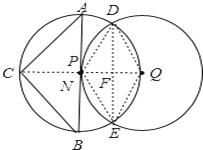
由已知PD=PQ=DQ，

∴△DPQ是等边三角形．

∴∠DQP=60°．

同理∠EQP=60°．

∴∠DQE=120°，

∵⊙P和⊙Q交于D、E，

∴QP⊥DE，DF=EF，

∵△EPQ是等边三角形，

∴∠QDE=30°，

∴FQ= DQ=1，

由勾股定理得：DF= =EF，

即ED=2 ，

S弓形DPE=S扇形QDE﹣S△DQE

= ﹣ ×2 ×1

= ﹣ ，

故月牙形公园的面积=4π﹣2（ π﹣ ）=（ π﹢2 ）km2．

答：月牙形公园的面积为（ π﹢2 ）km2

（2）

解：∵∠C=90°，

∴AB是⊙P的直径，

过点C作CN⊥AB于点N，S△ABC= CNAB，

∵AB=4km，

∴S△ABC的面积取最大值就是CN长度取最大值，即CN=CP=2km，

S△ABC的面积最大值等于4km2，

故场地的最大面积为4km2

【解析】（1）连接DQ、EQ、PD、PE、PQ、DE，得出等边三角形DPQ和等边三角形EPQ，得出∠PQD=∠EQP=60°，根据相交两圆的性质得出DE⊥PQ，求出FQ和DF的值，求出DE，分别求出扇形DQE的面积和三角形DEQ的面积，即可求出弓形DPE的面积，根据圆的面积和弓形的面积求出答案即可；（2）根据∠ACB=90°得出AB是圆的直径，是2km，要使三角形ABC的面积最大得出只要高CN最大即可，得出CN的最大值是CP（P和N重合，CN最大），代入求出即可．