
【题目】已知,如图①,∠MON=60°,点A,B为射线OM,ON上的动点(点A,B不与点O重合),且AB=4 ![]() ,在∠MON的内部,△AOB的外部有一点P,且AP=BP,∠APB=120°.
,在∠MON的内部,△AOB的外部有一点P,且AP=BP,∠APB=120°.
(1)求AP的长;
(2)求证:点P在∠MON的平分线上.
(3)如图②,点C,D,E,F分别是四边形AOBP的边AO,OB,BP,PA的中点,连接CD,DE,EF,FC,OP.
①当AB⊥OP时,请直接写出四边形CDEF的周长的值;
②若四边形CDEF的周长用t表示,请直接写出t的取值范围.
【答案】
(1)
解:如图
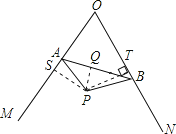
过点P作PQ⊥AB于点Q.
∵PA=PB,∠APB=120°,AB=4 ![]()
∴AQ=BQ=2 ![]() ,∠APQ=60°(等腰三角形的“三线合一”的性质),
,∠APQ=60°(等腰三角形的“三线合一”的性质),
在Rt△APQ中,sin∠APQ= ![]()
∴AP= ![]() =
= ![]() =
= ![]() =4
=4
(2)
证明:过点P分别作PS⊥OM于点S,PT⊥ON于点T.∴∠OSP=∠OTP=90°(垂直的定义);
在四边形OSPT中,∠SPT=360°﹣∠OSP﹣∠SOB﹣∠OTP=360°﹣90°﹣60°﹣90°=120°,
∴∠APB=∠SPT=120°,∴∠APS=∠BPT;
又∵∠ASP=∠BTP=90°,AP=BP,
∴△APS≌△BPT,
∴PS=PT(全等三角形的对应边相等)
∴点P在∠MON的平分线上;
(3)
解:①∵OP平分∠AOB,∠AOB=60°,OP⊥AB,
∴AQ=BQ= ![]() AB=2
AB=2 ![]() ,
,
∴OQ= ![]() =6,
=6,
同理:PQ= ![]() =2,
=2,
∴OP=8,
∵点C,D,E,F分别是四边形AOBP的边AO,OB,BP,PA的中点,
∴CD=EF= ![]() AB,CF=DE=
AB,CF=DE= ![]() OP,
OP,
∴四边形CDEF的周长为:8+4 ![]()
②CD和EF是△ABO和△ABP的中位线,
则CD=EF= ![]() AB=2
AB=2 ![]() ,
,
CF和DE分别是△AOP和△BOP的中位线,则CF=DE= ![]() OP,
OP,
当AB⊥OP时,OP为四点边形AOBP外接圆的直径时,OP最大,其值是8,OP一定大于当点A或B与点O重合时的长度是4.
则4+4 ![]() <t≤8+4
<t≤8+4 ![]()
【解析】(1)过点P作PQ⊥AB于点Q.根据等腰三角形的“三线合一”的性质推知AQ=BQ= ![]() AB,然后在直角三角形中利用特殊角的三角函数的定义可以求得AP的长度;(2)作辅助线PS、PT(过点P分别作PS⊥OM于点S,PT⊥ON于点T)构建全等三角形△APS≌△BPT;然后根据全等三角形的性质推知PS=PT;最后由角平分线的性质推知点P在∠MON的平分线上;(3)利用三角形中位线定理知四边形CDEF的周长的值是OP+AB.①当AB⊥OP时,根据直角三角形中锐角三角函数的定义可以求得OP的长度;②当AB⊥OP时,OP取最大值,即四边形CDEF的周长取最大值;当点A或B与点O重合时,四边形CDEF的周长取最小值.
AB,然后在直角三角形中利用特殊角的三角函数的定义可以求得AP的长度;(2)作辅助线PS、PT(过点P分别作PS⊥OM于点S,PT⊥ON于点T)构建全等三角形△APS≌△BPT;然后根据全等三角形的性质推知PS=PT;最后由角平分线的性质推知点P在∠MON的平分线上;(3)利用三角形中位线定理知四边形CDEF的周长的值是OP+AB.①当AB⊥OP时,根据直角三角形中锐角三角函数的定义可以求得OP的长度;②当AB⊥OP时,OP取最大值,即四边形CDEF的周长取最大值;当点A或B与点O重合时,四边形CDEF的周长取最小值.
【考点精析】通过灵活运用角平分线的性质定理和三角形中位线定理,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半即可以解答此题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
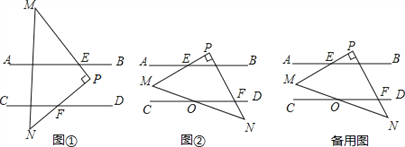
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,实线部分为某月牙形公园的轮廓示意图,它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成,⊙P与⊙Q的半径都是2km,点P在⊙Q上.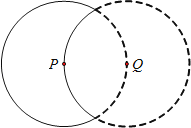
(1)求月牙形公园的面积;
(2)现要在公园内建一块顶点都在⊙P上的直角三角形场地ABC,其中∠C=90°,求场地的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨9 000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量比第一次的2倍还多300 kg.如果超市按9元/kg的价格出售,当大部分干果售出后,余下的600 kg按售价的八折售完.
(1)该种干果第一次的进价是多少?
(2)超市销售这种干果共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一边长为![]() 的正方形纸板的四个角各剪去一个边长为
的正方形纸板的四个角各剪去一个边长为![]() 的小正方形,然后把它折成一个无盖纸盒.
的小正方形,然后把它折成一个无盖纸盒.
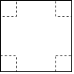
![]() 求该纸盒的体积;
求该纸盒的体积;
![]() 求该纸盒的全面积(外表面积);
求该纸盒的全面积(外表面积);
![]() 为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),求此时
为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),求此时![]() 与
与![]() 之间的倍数关系.(直接写出答案即可)
之间的倍数关系.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=10cm,则AB+BD=cm.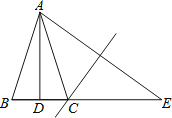
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边为a、b、c,由下列条件不能判断它是直角三角形的是( )
A. ∠A: ∠B: ∠C =3∶4∶5 B. ∠A=∠B+∠C
C. a2=(b+c)(b-c) D. a:b:c =1∶2∶![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生到离学校15千米的兴化生态园进行春季社会实践活动,先遣队与大队同时出发,先遣队的速度是大队速度的1.2倍,结果先遣队比大队早到30分钟,求先遣队的速度和大队速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com