
【题目】某中学组织学生到离学校15千米的兴化生态园进行春季社会实践活动,先遣队与大队同时出发,先遣队的速度是大队速度的1.2倍,结果先遣队比大队早到30分钟,求先遣队的速度和大队速度.
科目:初中数学 来源: 题型:
【题目】已知,如图①,∠MON=60°,点A,B为射线OM,ON上的动点(点A,B不与点O重合),且AB=4 ![]() ,在∠MON的内部,△AOB的外部有一点P,且AP=BP,∠APB=120°.
,在∠MON的内部,△AOB的外部有一点P,且AP=BP,∠APB=120°.
(1)求AP的长;
(2)求证:点P在∠MON的平分线上.
(3)如图②,点C,D,E,F分别是四边形AOBP的边AO,OB,BP,PA的中点,连接CD,DE,EF,FC,OP.
①当AB⊥OP时,请直接写出四边形CDEF的周长的值;
②若四边形CDEF的周长用t表示,请直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队(有甲、乙两组)承接了世界园艺博览会的一项小型工程任务,这项任务规定在若干天内完成.已知甲组单独完成这项工程所需时间比规定时间多20天,乙组单独完成这项工程所需时间比规定时间多10天.如果甲、乙两组先合作15天,剩下的由甲单独做,则正好如期完成,那么规定的时间是多少天?(列方程解应用题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某班研究性学习小组在一次综合实践活动中发现如下问题:在楼底的B处测得河对岸大厦上悬挂的条幅底端D的仰角为26°,在楼顶A处测得条幅顶端C的仰角为50°.若楼AB高度为18米,条幅CD长度为46米,请你帮助他们求出楼与大厦之间的距离BE及大厦的高度CE.(参考数据:sin26°≈0.44,sin50°≈0.77,tan26°≈0.49,tan50°≈1.19).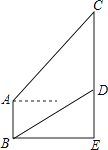
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB'C',若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是( )
A.![]()
π
B.![]()
π
C.2π
D.4π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3交y轴于点C,直线l为抛物线的对称轴,点P在第三象限且为抛物线的顶点.P到x轴的距离为 ![]() ,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B.
,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B. 
(1)求抛物线的表达式;
(2)直线y= ![]() x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y=
x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y= ![]() x+m的表达式;
x+m的表达式;
(3)若N为平面直角坐标系内的点,在直线y= ![]() x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC各顶点的坐标分A(-2,-2),B(-4,-1),C(-4,-4).

(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在
△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com