
【题目】某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:![]() ≈1.4)( )
≈1.4)( )
A.
B.
C.
D.
【答案】B
【解析】解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,
则∠EHG=∠HEF=90°,
∵∠AEF=135°,
∴∠AEH=∠AEF﹣∠HEF=45°,
∠EAH=45°,
在△EAH中,∠EHA=90°,∠EAH=45°,AE=1.3米,
∴EH=AEsin∠EAH≈1.3×0.7=0.91(米),
∵AB=1.3米,
∴AB+EH≈1.3+0.91=1.92≈2.2米.
故选B.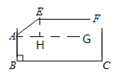
过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.先求出∠AEH=45°,则∠EAH=45°,然后在△EAH中,利用正弦函数的定义得出EH=AEsin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.


科目:初中数学 来源: 题型:
【题目】已知O为直线AB上一点,∠COE是直角,OF平分∠AOE.
(1)如图①,若∠COF=34°,则∠BOE=________;若∠COF=n°,则∠BOE=________;∠BOE与∠COF的数量关系为________________.
(2)当射线OE绕点O逆时针旋转到如图②的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
(3)在图③中,若∠COF=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半?若存在,请求出∠BOD的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.
(1)设x天后每千克该海鲜的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批海鲜一次性出售.设这批海鲜的销售总额为P元,试写出P与x之间的函数关系式;
(3)小李将这批海鲜存放多少天后出售可获得最大利润,最大利润是多少元?(利润W=销售总额﹣收购成本﹣各种费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c满足![]()
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A、B两种上网学习的月收费方案:
A方案:月租7元,可上网25小时,若超时,超出部分按每分钟0.01元收费;
B方案:月租10元,可上网50小时,若超时,超出部分按每分钟0.01元收费;
设每月上网学习时间为![]() 小时.
小时.
(1)当![]() >50时,用含有x的代数式分别表示A、B两种上网的费用;
>50时,用含有x的代数式分别表示A、B两种上网的费用;
(2)当x=100时,分别求出两种上网学习的费用.
(3)若上网40小时,选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.
小芸的作法如下:
①取AB=c,作AB的垂直平分线交AB于点O;
②以点O为圆心,OB长为半径画圆;
③以点B为圆心,a长为半径画弧,与⊙O交于点C;
④连接BC,AC.
则Rt△ABC即为所求.
老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是 
查看答案和解析>>
科目:初中数学 来源: 题型:
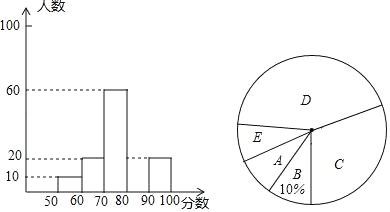
【题目】2018“体彩杯”重庆开州汉丰湖半程马拉松赛开跑前一周,某校七年级数学研究学习小组在某十字路口随机调查部分市民对“半马拉松赛”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
A | 50<n≤60 |
B | 60<n≤70 |
C | 70<n≤80 |
D | 80<n≤90 |
E | 90<n≤100 |
(1)本次调查的总人数为 人,在扇形统计图中“C”所在扇形的圆心角的度数为 度;
(2)补全频数分布图;
(3)若在这一周里,该路口共有7000人通过,请估计得分超过80的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
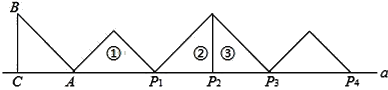
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=![]() ;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=
;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=![]() +1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=
+1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=![]() +2…按此规律继续旋转,直至得到点
+2…按此规律继续旋转,直至得到点![]() 为止,则
为止,则![]() =________.
=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com