
分析 首先将括号里面通分运算,进而利用分式混合运算法则计算得出答案,再解方程得出m的值,进而得出答案.
解答 解:$\frac{m-3}{3{m}^{2}-6m}$÷(m+2-$\frac{5}{m-2}$)
=$\frac{m-3}{3m(m-2)}$÷[$\frac{(m+2)(m-2)}{m-2}$-$\frac{5}{m-2}$]
=$\frac{m-3}{3m(m-2)}$÷$\frac{(m+3)(m-3)}{m-2}$
=$\frac{m-3}{3m(m-2)}$×$\frac{m-2}{(m+3)(m-3)}$
=$\frac{1}{3m(m+3)}$,
x2-3x+2=0,
解得:x1=1,x2=2,
当m=2时,不合题意舍去,
故m=1,则原式=$\frac{1}{3×1×4}$=$\frac{1}{12}$.
点评 此题主要考查了分式的化简求值以及一元二次方程的解法,正确掌握分式的混合运算法则是解题关键.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
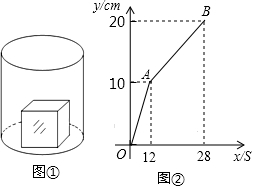 如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,CD与⊙O相切于点D,CD⊥AC于C,AC交⊙O于E,CD=2CE.
如图,AB为⊙O的直径,CD与⊙O相切于点D,CD⊥AC于C,AC交⊙O于E,CD=2CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
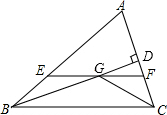 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知正方形ABCD,AB=3,点E在线段AB上,AE=1连结DE,DE的垂直平分线交DE于点P,交DC的延长线于点Q,PQ交BC于点G,连结EQ,EQ交BC于点F,连结GE.
如图,已知正方形ABCD,AB=3,点E在线段AB上,AE=1连结DE,DE的垂直平分线交DE于点P,交DC的延长线于点Q,PQ交BC于点G,连结EQ,EQ交BC于点F,连结GE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com