练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为84°、30°，则∠ACB的度数为（　　）
    A．14°B．27°C．28°D．54°

    分析 根据量角器测角度的方法得到∠AOB=58°，然后根据圆周角定理求解．

    解答 解：连结OA、OB，如图，
    ∵点A、B的读数分别为84°，30°，
    ∴∠AOB=84°-30°=54°，
    ∴∠ACB=$\frac{1}{2}$∠AOB=27°．
    故选B．

    点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．会使用量角器是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

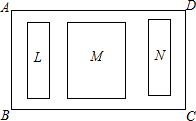    12．要对一块长60m．宽40m的矩形荒地ABCD（BC＞AB）进行绿化和硬化，设计方案如图所示．矩形L、M、N为三块绿地．其余为硬化路面，L、M、N三块绿地周围的硬化路面宽都相等．并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$．
    （1）求L、M、N三块绿地周围的硬化路面的宽；
    （2）若硬化路面费用为每平方米10元，绿化费用每平方米20元，则将这块荒地进行绿化和硬化完所需的费用为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．一个两位数，个位数字是十位数字的3倍．如果把个位数字与十位数字对调．那么得到的新数比原数大54．求原来的两位数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知△ABC≌△DEF，AB=2，AC=4，△DEF的周长为偶数，则EF的长为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．在△ABC和△A'B'C'中，下面能得到△ABC≌△A'B'C'的条件是（　　）
    A．AB=A'B'，AC=A'C，∠B=∠B'B．AB=A'B'，BC=B'C，∠A=∠A'
    C．AC=A'C'，BC=B'C'，∠C=∠C'D．AC=A'C'，BC=B'C'，∠B=∠B'

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．在-2，+（-3.5），0，$-\frac{2}{3}$，-（-0.7），11中，负分数有（　　）
    A．l个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．已知，△ABC≌△DEF，∠A=50°，∠B=60°，∠C=70°，则∠F的度数为（　　）
    A．50°B．60°C．70°D．80°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下列说法正确的是（　　）
    A．三角形外接圆的圆心是三边中线的交点
    B．三角形外接圆的圆心是内角平分线的交点
    C．三角形外接圆的圆心是三边垂直平分线的交点
    D．三角形外接圆的圆心是三条高的交点

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

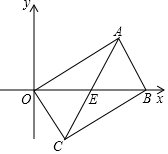    4．定义：如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“特征轴三角形”．显然，“特征轴三角形”是等腰三角形．
    （1）抛物线y=$\frac{1}{2}$x2-2对应的“特征轴三角形”是④；抛物线y=x2-2$\sqrt{3}$x对应的“特征轴三角形”是②．（把下列较恰当结论的序号填在横线上：①腰与底边不相等的等腰三角形；②等边三角形；③非等腰的直角三角形；④等腰直角三角形．）
    （2）若抛物线y=ax2+2ax-3a对应的“特征轴三角形”是直角三角形，则a的值为±$\frac{1}{2}$．
    （3）如图，面积为12$\sqrt{3}$的矩形ABCO的对角线OB在x轴的正半轴上，AC与OB相交于点E，若△ABE是抛物线y=ax2+bx+c的“特征轴三角形”，求此抛物线的解析式．

    查看答案和解析>>

    同步练习册答案