
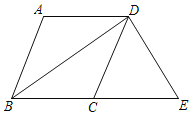
【题目】如图,面积为24的ABCD中,对角线BD平分∠ABC,过点D作DE⊥BD交BC的延长线于点E,DE=6,则sin∠DCE的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
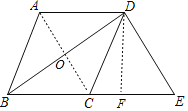
连接AC,过点D作DF⊥BE于点E,由BD平分∠ABC证得四边形ABCD是菱形,利用DE⊥BD得到OC∥ED求出AC,根据ABCD面积为24求出BD,再由勾股定理求出BC,设CF=x,则BF=5+x,利用BD2﹣BF2=DC2﹣CF2求出x得到DF,即可求出答案.
解:连接AC,过点D作DF⊥BE于点E,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵![]() ABCD中,AD∥BC,
ABCD中,AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠ABD,
∴AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,OB=OD,
∵DE⊥BD,
∴OC∥ED,
∵DE=6,
∴OC=![]() ,
,
∴AC=6,
∵![]() ABCD的面积为24,
ABCD的面积为24,
∴![]() ,
,
∴BD=8,
∴![]() =
=![]() =5,
=5,
设CF=x,则BF=5+x,
由BD2﹣BF2=DC2﹣CF2可得:82﹣(5+x)2=52﹣x2,
解得x=![]() ,
,
∴DF=![]() ,
,
∴sin∠DCE=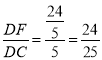 .
.
故选:A.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与x轴交于A(﹣2,0)、B(4,0)两点,且函数经过点(3,10).
(1)求二次函数的解析式;
(2)设这个二次函数的顶点为P,求△ABP的面积;
(3)当x为何值时,y≤0.(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“小组合作制”正在七年级如火如茶地开展,旨在培养七年级学生的合作学习的精神和能力,学会在合作中自主探索.数学课上,吴老师在讲授“角平分线”时,设计了如下四种教学方法:①教师讲授,学生练习;②学生合作交流,探索规律;③教师引导学生总结规律,学生练习;④教师引导学生总结规律,学生合作交流,吴老师将上述教学方法作为调研内容发到七年级所有同学手中要求每位同学选出自己最喜欢的一种,然后吴老师从所有调查问卷中随机抽取了若干份调查问卷作为样本,统计如下:
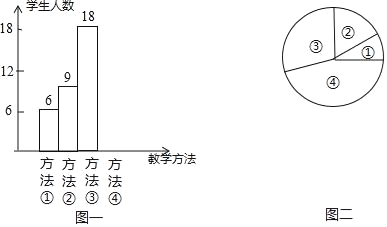
序号①②③④代表上述四种教学方法,图二中,表示①部分的扇形的中心角度数为36°,请回答问题:
(1)在后来的抽样调查中,吴老师共抽取 位学生进行调查;并将条形统计图补充完整;
(2)图二中,表示③部分的扇形的中心角为多少度?
(3)若七年级学生中选择④种教学方法的有540人,请估计七年级总人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年,中央全面落实“稳房价”的长效管控机制,重庆房市较上一年大幅降温,11月,LH地产共推出了大平层和小三居两种房型共80套,其中大平层每套面积180平方米,单价1.8万元/平方米,小三居每套面积120平方米,单价1.5万元/平方米.
(1)LH地产11月的销售总额为18720万元,问11月要推出多少套大平层房型?
(2)2019年12月,中央经济会议上重申“房子是拿来住的,不是拿来炒的”,重庆房市成功稳定并略有回落.为年底清盘促销,LH地产调整营销方案,12月推出两种房型的总数量仍为80套,并将大平层的单价在原有基础上每平方米下调![]() 万元(m>0),将小三居的单价在原有基础上每平方米下调
万元(m>0),将小三居的单价在原有基础上每平方米下调![]() 万元,这样大平层的销量较(1)中11月的销量上涨了7m套,且推出的房屋全部售罄,结果12月的销售总额恰好与(1)中I1月的销售总额相等.求出m的值.
万元,这样大平层的销量较(1)中11月的销量上涨了7m套,且推出的房屋全部售罄,结果12月的销售总额恰好与(1)中I1月的销售总额相等.求出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
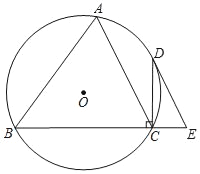
【题目】如图,△ABC内接于⊙O,过点C作BC的垂线交⊙O于D,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;
(4)身高在![]() 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
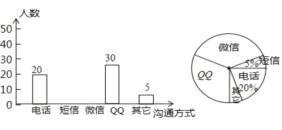
(1)在扇统计图中,表示“QQ”的扇形圆心角的度数为_____;根据这次统计数据了解到最受学生欢迎的沟通方式是______.
(2)将条形统计图补充完整;
(3)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() 点
点![]() 为
为![]() 的中点,以
的中点,以![]() 为底边的等腰
为底边的等腰![]() 按如图所示位置摆放,且
按如图所示位置摆放,且![]() .请仅用无刻度的直尺分别按下列要求作图(保留作图痕迹).
.请仅用无刻度的直尺分别按下列要求作图(保留作图痕迹).
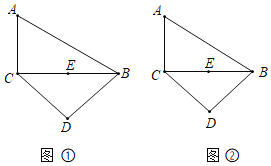
![]() 如图①,在
如图①,在![]() 上求作一点
上求作一点![]() ,使四边形
,使四边形![]() 为菱形;
为菱形;
![]() 如图②,过点
如图②,过点![]() 作线段
作线段![]() 使得线段
使得线段![]() 将
将![]() 的面积平分.
的面积平分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com