
ҰңМвДүҰүЛжЧЕНЁС¶әәКхСёГН·ұХ№Ә¬ИЛУлИЛЦ®әдµД№µНЁ·ҢКҢёь¶аСщҰұ±гҢЭӘ®ДіРӘКэС§РЛИ¤РҰЧйЙиәЖБЛҰ°ДгЧоПІ»¶µД№µНЁ·ҢКҢҰ±µчІйОКңн(ГүИЛ±ШСҰЗТЦ»СҰТ»ЦЦ)Ә¬ФЪИ«РӘ·¶О§ДЪЛж»ъµчІйБЛІү·ЦС§ЙъӘ¬Ң«НіәЖҢб№ы»жЦЖБЛИзПВБҢ·щІ»НкХыµДНіәЖНәӘ¬ЗлҢбғПНәЦРЛщёшµДРЕПұҢвөрПВБРОКМвӘғ
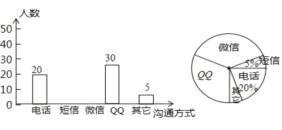
ӘЁ1Ә©ФЪЙИНіәЖНәЦРӘ¬±нКңҰ°QQҰ±µДЙИРОФІРДҢЗµД¶ИКэОҒ_____Ә»ёщңЭХвөОНіәЖКэңЭБЛҢвµҢЧоКЬС§Йъ»¶УµД№µНЁ·ҢКҢКЗ______Ә®
ӘЁ2Ә©Ң«МхРОНіәЖНәІ№ідНкХыӘ»
ӘЁ3Ә©ДіМмәЧҰұТТБҢГыН¬С§¶әПлөУҰ°ОұРЕҰ±ҰұҰ°QQҰ±ҰұҰ°µз»°Ұ±ИэЦЦ№µНЁ·ҢКҢЦРСҰТ»ЦЦ·ҢКҢУл¶Ф·ҢБҒПµӘ¬УГБР±н»т»КчЧөНәµД·Ң·ЁЗуіцәЧҰұТТБҢГыН¬С§ЗҰғГСҰЦРН¬Т»ЦЦ№µНЁ·ҢКҢµДёЕВКӘ®
Ұңөр°ёҰүӘЁ1Ә©108ҰгӘ¬ОұРЕӘ»ӘЁ2Ә©әыҢвОцӘ»ӘЁ3Ә©![]()
ҰңҢвОцҰү
ӘЁ1Ә©ёщңЭПІ»¶µз»°№µНЁµДИЛКэУл°Щ·Ц±ИәөүЙЗуіц№ІійІйИЛКэӘ¬ЗуіцК№УГQQµД°Щ·Ц±ИәөүЙЗуіцQQµДЙИРОФІРДҢЗ¶ИКэӘ¬ёщңЭЧЬИЛКэә°ЛщХә°Щ·Ц±ИәөүЙЗуіцК№УГ¶МРЕµДИЛКэӘ¬ЧЬИЛКэәхИӨіэОұРЕЦ®НвµДЛДЦЦ·ҢКҢµДИЛКэәөүЙµГµҢК№УГОұРЕµДИЛКэӘ®
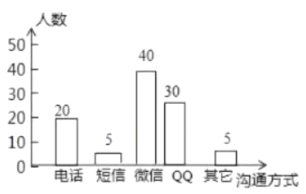
ӘЁ2Ә©ёщңЭ¶МРЕУлОұРЕµДИЛКэәөүЙІ№И«МхРОНіәЖНәӘ®
ӘЁ3Ә©БРіцКчЧөНә·Ц±рЗуіцЛщУРЗйүцТФә°әЧҰұТТБҢГыН¬С§ЗҰғГСҰЦРН¬Т»ЦЦ№µНЁ·ҢКҢµДЗйүцғуӘ¬АыУГёЕВК№«КҢәөүЙЗуіцәЧҰұТТБҢГыН¬С§ЗҰғГСҰЦРН¬Т»ЦЦ№µНЁ·ҢКҢµДёЕВКӘ®
ҢвӘғӘЁ1Ә©ПІ»¶УГµз»°№µНЁµДИЛКэОҒ20Ә¬ЛщХә°Щ·Ц±ИОҒ20%Ә¬
ҰаөЛөО№ІійІйБЛӘғ20ҰВ20%ӘҢ100ИЛ
ПІ»¶УГQQ№µНЁЛщХә±ИАэОҒӘғ![]() Ә¬
Ә¬
ҰаҰ°QQҰ±µДЙИРОФІРДҢЗµД¶ИКэОҒӘғ360ҰгҰБ![]() ӘҢ108ҰгӘ¬
ӘҢ108ҰгӘ¬
ПІ»¶УГ¶МРЕµДИЛКэОҒӘғ100ҰБ5%ӘҢ5ӘЁИЛӘ©
ПІ»¶УГОұРЕµДИЛКэОҒӘғ100205305ӘҢ40ӘЁИЛӘ©Ә¬
ҰаЧоКЬС§Йъ»¶УµД№µНЁ·ҢКҢКЗӘғОұРЕӘ¬
№Көр°ёОҒӘғ108ҰгӘ¬ОұРЕӘ»
ӘЁ2Ә©І№И«МхРОНәИзПВӘғ
ӘЁ3Ә©БРіцКчЧөНәӘ¬ИзНәЛщКң
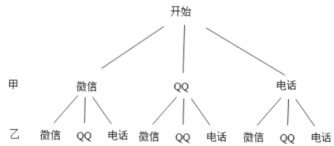
ЛщУРЗйүц№ІУР9ЦЦЗйүцӘ¬ЖдЦРБҢИЛЗҰғГСҰЦРН¬Т»ЦЦ№µНЁ·ҢКҢ№ІУР3ЦЦЗйүцӘ¬
әЧҰұТТБҢГыН¬С§ЗҰғГСҰЦРН¬Т»ЦЦ№µНЁ·ҢКҢµДёЕВКОҒӘғ![]() Ә®
Ә®



| Дкә¶ | ёЯЦРүОіМ | Дкә¶ | іхЦРүОіМ |
| ёЯТ» | ёЯТ»Гв·СүОіМНЖәцӘҰ | іхТ» | іхТ»Гв·СүОіМНЖәцӘҰ |
| ёЯ¶ю | ёЯ¶юГв·СүОіМНЖәцӘҰ | іх¶ю | іх¶юГв·СүОіМНЖәцӘҰ |
| ёЯИэ | ёЯИэГв·СүОіМНЖәцӘҰ | іхИэ | іхИэГв·СүОіМНЖәцӘҰ |
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүТСЦҒЦ±ПЯ![]() Ул
Ул![]() ЦбҢ»УЪµг
ЦбҢ»УЪµг![]() Ә¬ЗТ№эЕЧОпПЯ
Ә¬ЗТ№эЕЧОпПЯ![]() µД¶Өµг
µД¶Өµг![]() ғНЕЧОпПЯЙПµДБнТ»µг
ғНЕЧОпПЯЙПµДБнТ»µг![]() .
.
ӘЁ1Ә©Ифµг![]()
ұЩЗуЕЧОпПЯҢвОцКҢӘ»
ұЪИф![]() Ә¬ЗуЦ±ПЯҢвОцКҢ.
Ә¬ЗуЦ±ПЯҢвОцКҢ.
ӘЁ2Ә©Иф![]() Ә¬№эµг
Ә¬№эµг![]() Чч
Чч![]() ЦбµДЖҢРРПЯУлЕЧОпПЯµД¶ФіЖЦбҢ»УЪµг
ЦбµДЖҢРРПЯУлЕЧОпПЯµД¶ФіЖЦбҢ»УЪµг![]() Ә¬µ±
Ә¬µ±![]() К±Ә¬Зу
К±Ә¬Зу![]() µДГж»э
µДГж»э![]() µДЧоөуЦµ.
µДЧоөуЦµ.
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
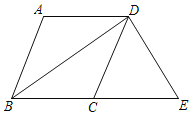
ҰңМвДүҰүИзНәӘ¬Гж»эОҒ24µДABCDЦРӘ¬¶ФҢЗПЯBDЖҢ·ЦҰПABCӘ¬№эµгDЧчDEҰНBDҢ»BCµДСУі¤ПЯУЪµгEӘ¬DEӘҢ6Ә¬ФтsinҰПDCEµДЦµОҒӘЁҰҰҰҰӘ©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүДіРӘЧйЦҮБЛТ»өОЖЯДкә¶үЖәәРҰЦЖЧч±ИИьӘ¬УРAҰұBҰұCҰұDЛДёц°а№ІМṩБЛ100әюІОИьЧчЖ·Ә¬C°аМṩµДІОИьЧчЖ·µД»сҢ±ВКОҒ50%Ә¬ЖдЛыәёёц°аµДІОИьЧчЖ·Зйүцә°»сҢ±Зйүц»жЦЖФЪПВБРНәұЩғННәұЪБҢ·щЙРІ»НкХыµДНіәЖНәЦР.
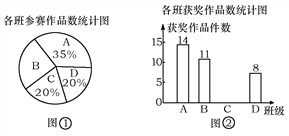
ӘЁ1Ә©B°аІОИьЧчЖ·УР¶аЙЩәюӘү
ӘЁ2Ә©ЗлДгҢ«НәұЪµДНіәЖНәІ№ідНкХыӘ»
ӘЁ3Ә©НЁ№эәЖЛгЛµГчӘ¬ДДёц°аµД»сҢ±ВКёЯӘү
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүИзНәACӘ¬BDКЗҰСOµДБҢМхЦ±ң¶Ә¬КЧО»ЛіөОБ¬ҢУAӘ¬BӘ¬CӘ¬DµГµҢЛД±ЯРОABCDӘ¬ИфAD=3Ә¬ҰПBAC=30ҰгӘ¬ФтНәЦРТхУ°Іү·ЦµДГж»эКЗ______Ә®

Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүТСЦҒЕЧОпПЯ y x2 mx 2m 4ӘЁm>0Ә©Ә®
ӘЁ1Ә©Ц¤ГчӘғёГЕЧОпПЯУл x ЦбЧЬУРБҢёцІ»Н¬µДҢ»µгӘ»
ӘЁ2Ә©ЙиёГЕЧОпПЯУл x ЦбµДБҢёцҢ»µг·Ц±рОҒ AӘ¬BӘЁµг A ФЪµг B µДУТІа)Ә¬Ул y ЦбҢ»УЪµг CӘ¬AӘ¬BӘ¬Иэµг¶әФЪФІ P ЙПӘ®
ұЩИфТСЦҒ BӘЁ-3Ә¬0Ә©Ә¬ЕЧОпПЯЙПөжФЪТ»µг M К№ҰчABM µДГж»эОҒ 15Ә¬Зуµг M µДЧш±кӘ»
ұЪКФЕР¶ПӘғІ»ВЫ m ИҰИОғОХэКэӘ¬ФІ P КЗ·сң№э y ЦбЙПДіёц¶ЁµгӘүИфКЗӘ¬ЗуіцёГ¶ЁµгµДЧш±кӘ¬ИфІ»КЗӘ¬ЛµГчАнУЙӘ®
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүИзНәӘ¬ҰСOЦРӘ¬ABӘҢACӘ¬ҰПACBӘҢ75ҰгӘ¬BCӘҢ1Ә¬ФтТхУ°Іү·ЦµДГж»эКЗӘЁҰҰҰҰӘ©
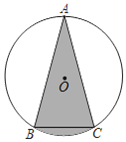
A.1+![]() ¦РB.
¦РB.![]() ¦РC.
¦РC.![]() ¦РD.1+
¦РD.1+![]() ¦Р
¦Р
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүИзНәӘ¬ЕЧОпПЯy=ax2+bx+cң№эµгAӘЁ©Ѓ2Ә¬5Ә©Ә¬УлxЦбПаҢ»УЪBӘЁ©Ѓ1Ә¬0Ә©Ә¬CӘЁ3Ә¬0Ә©БҢµгӘ®
ӘЁ1Ә©ЗуЕЧОпПЯµДғҮКэ±нөпКҢӘ»
ӘЁ2Ә©µгDФЪЕЧОпПЯµД¶ФіЖЦбЙПӘ¬ЗТО»УЪxЦбµДЙП·ҢӘ¬Ң«ҰчBCDСШЦ±ПЯBD·ХЫµГµҢҰчBCҰдDӘ¬ИфµгCҰдЗҰғГВдФЪЕЧОпПЯµД¶ФіЖЦбЙПӘ¬ЗуµгCҰдғНµгDµДЧш±кӘ»

Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүИзНәӘ¬ТФҰчABCµД±ЯACОҒЦ±ң¶µДҰСOЗҰОҒҰчABCµДНвҢУФІӘ¬ҰПABCµДЖҢ·ЦПЯҢ»ҰСOУЪµгDӘ¬№эµгDЧчDEҰОACҢ»BCµДСУі¤ПЯУЪµгEӘ®
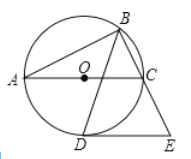
(1)ИфҰПBACӘҢ28Ұг20ҰдӘ¬ФтҰПEӘҢ Ә»
(2)ЗуЦ¤ӘғDEКЗҰСOµДЗРПЯӘ»
(3)ИфtanҰПACBӘҢ2 Ә¬BCӘҢ2![]() Ә¬ЗуDEµДі¤Ә®
Ә¬ЗуDEµДі¤Ә®
Ійүөөр°ёғНҢвОц>>
№ъәКС§РӘУЕСҰ - Б·П°ІбБР±н - КФМвБР±н
ғю±±КҰ»ӨБҒНшОӨ·ЁғНІ»БәРЕПұңЩ±ЁЖҢМЁ | НшЙПУРғ¦РЕПұңЩ±ЁЧЁЗш | µзРЕХ©ЖңЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРғ¦РЕПұңЩ±ЁЧЁЗш | ЙжЖуЗЦИЁңЩ±ЁЧЁЗш
ОӨ·ЁғНІ»БәРЕПұңЩ±Ёµз»°Әғ027-86699610 ңЩ±ЁУКПдӘғ58377363@163.com