
【题目】已知抛物线 y x2 mx 2m 4(m>0).
(1)证明:该抛物线与 x 轴总有两个不同的交点;
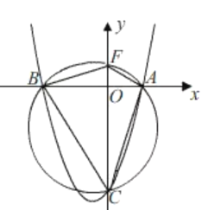
(2)设该抛物线与 x 轴的两个交点分别为 A,B(点 A 在点 B 的右侧),与 y 轴交于点 C,A,B,三点都在圆 P 上.
①若已知 B(-3,0),抛物线上存在一点 M 使△ABM 的面积为 15,求点 M 的坐标;
②试判断:不论 m 取任何正数,圆 P 是否经过 y 轴上某个定点?若是,求出该定点的坐标,若不是,说明理由.
【答案】(1)见解析;(2)①M![]() 或
或![]() 或
或![]() 或
或![]() ;②是,圆 P经过 y 轴上的定点(0,1).
;②是,圆 P经过 y 轴上的定点(0,1).
【解析】
(1)令y=0,证明![]() ,即可解答;
,即可解答;
(2)①将B(-3,0)代入y x2 mx 2m 4,求出抛物线解析式,求出点A的坐标,从而得到AB=5,根据△ABM 的面积为 15,列出方程解答即可;
②求出OA=2,OB=m+2,OC=2(m+2),判断出∠OCB=∠OAF,求出tan∠OCB=![]() ,即可求出OF=1,即可得出结论.
,即可求出OF=1,即可得出结论.
解:(1)当y=0时,x2 mx 2m 4=0
∴![]() ,
,
∵m>0,
∴![]() ,
,
∴该抛物线与 x 轴总有两个不同的交点;
(2)①将B(-3,0)代入y x2 mx 2m 4得:
![]() ,解得m=1,
,解得m=1,
∴y x2 x 6,
令y=0得:x2 x 6=0,解得:![]() ,
,
∴A(2,0),AB=5,
设M(n,n2 n 6)
则![]() ,即
,即![]()
解得:![]() ,
,
∴M![]() 或
或![]() 或
或![]() 或
或![]() .
.
②是,圆 P经过 y 轴上的定点(0,1),理由如下:
令y=0,
∴x2 mx 2m 4=0,即
![]() ,
,
∴![]() 或
或![]() ,
,
∴A(2,0),![]() ,
,
∴OA=2,OB=m+2,
令x=0,则y=-2(m+2),
∴OC=2(m+2),
如图,∵点A,B,C在圆P上,
∴∠OCB=∠OAF,
在Rt△BOC中,![]() ,
,
在Rt△AOF中,![]() ,
,
∴OF=1,
∴点F(0,1)
∴圆 P经过 y 轴上的定点(0,1).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
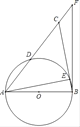
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的半圆分别交AC、BC于点D、E两点,BF与⊙O相切于点B,交AC的延长线于点F.
(1)求证:D是AC的中点;
(2)若AB=12,sin∠CAE=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
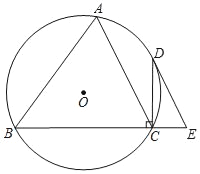
【题目】如图,△ABC内接于⊙O,过点C作BC的垂线交⊙O于D,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
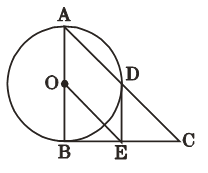
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:![]()
(3)若tanC=![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
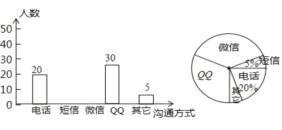
(1)在扇统计图中,表示“QQ”的扇形圆心角的度数为_____;根据这次统计数据了解到最受学生欢迎的沟通方式是______.
(2)将条形统计图补充完整;
(3)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣![]() x+8交x轴于点A,交y轴于点B,点C在AB上,AC=5,CD∥OA,CD交y轴于点D.
x+8交x轴于点A,交y轴于点B,点C在AB上,AC=5,CD∥OA,CD交y轴于点D.
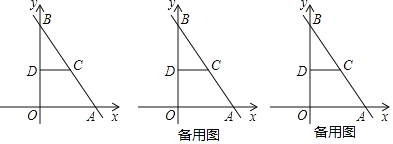
(1)求点D的坐标;
(2)点P从点O出发,以每秒1个单位长度的速度沿OA匀速运动,同时点Q从点A出发,以每秒![]() 个单位长度的速度沿AB匀速运动,设点P运动的时间为t秒(0<t<3),△PCQ的面积为S,求S与t之间的函数关系式;
个单位长度的速度沿AB匀速运动,设点P运动的时间为t秒(0<t<3),△PCQ的面积为S,求S与t之间的函数关系式;
(3)在(2)的条件下,过点Q作RQ⊥AB交y轴于点R,连接AD,点E为AD中点,连接OE,求t为何值时,直线PR与x轴相交所成的锐角与∠OED互余.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=
x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=![]() x2+bx+c经过点B,C,与x轴的另一个交点为点A.
x2+bx+c经过点B,C,与x轴的另一个交点为点A.
(1)求抛物线的解析式;
(2)点P是直线BC下方的抛物线上一动点,求四边形ACPB的面积最大时点P的坐标;
(3)若点M是抛物线上一点,请直接写出使∠MBC=![]() ∠ABC的点M的坐标.
∠ABC的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,若EB为∠AEG的平分线,EF和BC的延长线交于点H.下列结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤若![]() ,则
,则![]() .以上命题,正确的有( )
.以上命题,正确的有( )
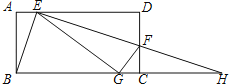
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com