
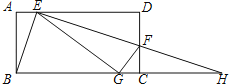
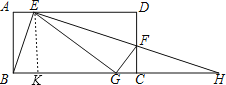
【题目】如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,若EB为∠AEG的平分线,EF和BC的延长线交于点H.下列结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤若![]() ,则
,则![]() .以上命题,正确的有( )
.以上命题,正确的有( )
A.2个B.3个C.4个D.5个
【答案】B
【解析】
①根据平角的定义,折叠的性质和角平分线的性质即可作出判断;
②根据折叠的性质和等腰三角形的性质可知DE≠CH;
③无法证明BE=EF;
④根据角平分线的性质,等腰三角形的性质和三角形中线的性质可得△BEG和△HEG的面积相等;
⑤过E点作EK⊥BC,垂足为K,在RT△EKG中利用勾股定理可做出判断.
解:①由折叠的性质可知∠DEF=∠GEF,∵EB为∠AEG的平分线,∴∠AEB=∠GEB,∵∠AED=180°,∴∠BEF=90°,故正确;
②根据矩形的性质可得∠D=∠FCH,∠DFE=∠CFH(对顶角相等)
所以△EDF∽△HCF,DF>CF,故DE≠CH,故错误;
③无法证明BE=EF,故错误;
④∵ABCD是矩形,
∴∠AEB=∠EBC(内错角相等)
又∵EB为∠AEG的平分线,
∴∠AEB=∠BEG,
∴∠BEG=∠EBC,
∴△GEB是等腰三角形,
∵ABCD是矩形,
∴∠DEF=∠CHF(内错角相等),
又∵折叠的性质得到∠DEF=∠FEG,
∴∠FEG=∠CHF,
∴△GEH是等腰三角形,
则G是BH边的中线,
∴△BEG和△HEG的面积相等,故正确;
⑤过E点作EK⊥BC,垂足为K.设BK=x,CD=y,由![]() 可得AD=2y
可得AD=2y
∵EB平分∠AEG,
∴∠AEB=∠BEG,
又∵AD∥BC,
∴∠AEB=∠EBG,
∴∠BEG=∠EBG,
∴BG=EG
在RT△EKG中,![]() ,
,![]() ,
,
![]() ,由勾股定理有
,由勾股定理有![]() ,即
,即![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,K、G重合,不符合题意,舍去。故取
,K、G重合,不符合题意,舍去。故取![]() ,此时
,此时![]() ,则
,则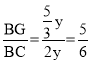 ,故正确的有3个.
,故正确的有3个.
故选:B.


科目:初中数学 来源: 题型:
【题目】某企业为了解饮料自动售卖机的销售情况,对甲、乙两个城市的饮料自动售卖机进行抽样调查,从两个城市中所有的饮料自动售卖机中分别抽取16台,记录下某一天各自的销售情况(单位:元)如下:
甲:25、45、38、22、10、28、61、18、38、45、78、45、58、32、16、78
乙:48、52、21、25、33、12、42、39、41、42、33、44、33、18、68、72
整理、描述数据:对销售金额进行分组,各组的频数如下:
销传金额 |
|
|
|
|
甲 | 3 | 6 | 4 | 3 |
乙 | 2 | 6 | a | b |
分析数据:两组样本数据的平均数、中位数如下表所示:
城市 | 中位数 | 平均数 | 众数 |
甲 | C | 39.8 | 45 |
乙 | 40 | 38.9 | d |
请根据以上信息,回答下列问题:
(1)填空:a=, b=, c=, d=.
(2)两个城市目前共有饮料自动售卖机4000台,估计日销售金额不低于40元的数量约为多少台?
(3)根据以上数据,你认为甲、乙哪个城市的饮料自动售卖机销售情况较好?请说明理由(一条理由即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 y x2 mx 2m 4(m>0).
(1)证明:该抛物线与 x 轴总有两个不同的交点;
(2)设该抛物线与 x 轴的两个交点分别为 A,B(点 A 在点 B 的右侧),与 y 轴交于点 C,A,B,三点都在圆 P 上.
①若已知 B(-3,0),抛物线上存在一点 M 使△ABM 的面积为 15,求点 M 的坐标;
②试判断:不论 m 取任何正数,圆 P 是否经过 y 轴上某个定点?若是,求出该定点的坐标,若不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
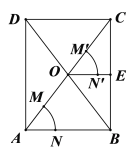
【题目】如图,平行四边形ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO,AB于点M,N;②以点O为圆心,以AM长为半径作弧,交OC于点M';③以点M'为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点N';④过点N'作射线ON'交BC于点E.若AB=8,则线段OE的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y= ![]() +(1-2a)x(a>0),下列说法错误的是( )
+(1-2a)x(a>0),下列说法错误的是( )
A. 当![]() 时,该二次函数图象的对称轴为y轴
时,该二次函数图象的对称轴为y轴
B. 当a>![]() 时,该二次函数图象的对称轴在y轴的右侧
时,该二次函数图象的对称轴在y轴的右侧
C. 该二次函数的图象的对称轴可为x=1
D. 当x>2时,y的值随x的值增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的项点为
的项点为![]() ,交
,交![]() 轴于
轴于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧),且
点左侧),且![]() .
.
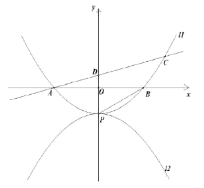
(1)求抛物线![]() 的函数解析式;
的函数解析式;
(2)过点![]() 的直线交抛物线于点
的直线交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 的面积被
的面积被![]() 轴分为1: 4两个部分,求直线
轴分为1: 4两个部分,求直线![]() 的解析式;
的解析式;
(3)在(2)的情况下,将抛物线![]() 绕点
绕点![]() 逆时针旋转180°得到抛物线
逆时针旋转180°得到抛物线![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,当点
上一点,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 为直角三角形?
为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com