
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��y����![]() x+8��x���ڵ�A����y���ڵ�B����C��AB�ϣ�AC��5��CD��OA��CD��y���ڵ�D��
x+8��x���ڵ�A����y���ڵ�B����C��AB�ϣ�AC��5��CD��OA��CD��y���ڵ�D��
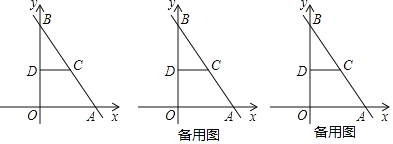
��1�����D�����ꣻ
��2����P�ӵ�O��������ÿ��1����λ���ȵ��ٶ���OA�����˶���ͬʱ��Q�ӵ�A��������ÿ��![]() ����λ���ȵ��ٶ���AB�����˶������P�˶���ʱ��Ϊt�루0��t��3������PCQ�����ΪS����S��t֮��ĺ�����ϵʽ��
����λ���ȵ��ٶ���AB�����˶������P�˶���ʱ��Ϊt�루0��t��3������PCQ�����ΪS����S��t֮��ĺ�����ϵʽ��
��3���ڣ�2���������£�����Q��RQ��AB��y���ڵ�R������AD����EΪAD�е㣬����OE����tΪ��ֵʱ��ֱ��PR��x���ཻ���ɵ��������OED���࣮
���𰸡���1��D��0��4������2��S=![]() t2��6t+12����3��t��
t2��6t+12����3��t��![]() ��
��![]()
��������
��1������֤��AC=BC������ƽ���ߵȷ��߶ζ����Ƴ�OD=BD=4���ɽ�����⣮
��2����ͼ2����PF��AB�ڵ�F�����PF��CQ���ɽ�����⣮
��3�����������Σ���R��y��ĸ������ϣ���ͼ3�У���R��y����������ϣ���ͼ4�У������ַ������OR���������̼��ɽ�����⣮
�⣺��1����ͼ1�У�
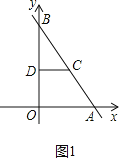
��ֱ��y����![]() x+8��x���ڵ�A����y���ڵ�B��
x+8��x���ڵ�A����y���ڵ�B��
��A��6��0����B��0��8��
��OA��6��OB��8��
��AB��![]() ��
��![]() ��10��
��10��
��AC��5��
��AC��BC��5��
��CD��OA��
��BD��OD��4��
��D��0��4����
��2����ͼ2����PF��AB�ڵ�F��PA��6��t
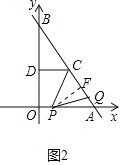
PF��PAsin��PAF��![]() ��6��t����
��6��t����
��CQ��5��![]() t��
t��
S��![]() CQPF��
CQPF��![]() ��5��
��5��![]() t��
t��![]() ��6��t����
��6��t����![]() t2��6t+12��
t2��6t+12��
��3����ͼ3�У���OG��AD �ڵ�G��
��Rt��AOD��AD��![]() ��
��![]() ��2
��2![]() ��
��
��S��AOD��![]() ODOA��
ODOA��![]() ADOG
ADOG
��OG��![]() ��
��![]() ��
��
��DG��![]() ��
��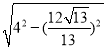 ��
��![]() ��
��
��DE��AE��![]() ��
��
��GE��DE��DG��![]() ��
��![]() ��
��![]() ��
��
�ߡ�OED+��OPR��90������OED+��EOG��90����
���OPR����EOG��
��tan��OPR��tan��EOG��![]()
��BR��![]() ��
�� ��
��![]() ��
��![]() t��
t��
��tan��OPR��![]() ��
��![]() ��OP��t��
��OP��t��
��OR��![]() t��
t��
��R��y��ĸ������ϣ���ͼ3�У�

OR��BR��8��![]() ��
��![]() t��
t��
��![]() t��
t��![]() ��
��![]() t��
t��
���t��![]() ��
��
��R��y����������ϣ���ͼ4�У�
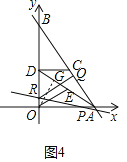
OR��8��BR��![]() t��
t��![]() ��
��
��![]() t��
t��![]() t��
t��![]() ��
��
���t��![]() ��
��
���ϣ���tֵΪ![]() ��
��![]() ��ֱ��PR��x���ཻ���ɵ��������OED���࣮
��ֱ��PR��x���ཻ���ɵ��������OED���࣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y��ax2+bx��3��a��0����x�ύ�ڵ�A����1��0���͵�B����OB��3OA����y�ύ�ڵ�C���������߶���Ϊ��D��
��1���������ߵı���ʽ����D�����ꣻ
��2�������E��y���ϵ�һ�㣨��E���C���غϣ�����BE��DEʱ�����E�����ꣻ
��3�������F���������ϵ�һ�㣮�ҡ�FBD��135�㣬���F�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��̽�����еĹ��ɣ���![]() +
+![]() ��1��
��1��![]() ����
����![]() +
+![]() ��
��![]() ��
��![]() ����
����![]() +
+![]() ��
��![]() ��
��![]() ����
����![]() +
+![]() ��
��![]() ��
��![]() ������
������
��1�������Ϲ���д���ڢ����ʽ��_______��
��2�����벢д����n����ʽ��_________��
��3����֤���������ȷ�ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������� OAB �Ķ��� O Ϊԭ�㣬�뾶 OB ���ڵ�ֱ��Ϊ x �ᣬ����ƽ��ֱ������ϵ���� B ������Ϊ(2��0)���������� ![]() (n Ϊ����)������ OAB �ı߽����������������� n ��ȡֵ��Χ��( )
(n Ϊ����)������ OAB �ı߽����������������� n ��ȡֵ��Χ��( )

A.n>-4B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ y x2 mx 2m 4��m>0����
��1��֤�������������� x ������������ͬ�Ľ��㣻
��2������������� x �����������ֱ�Ϊ A��B���� A �ڵ� B ���Ҳ�)���� y �ύ�ڵ� C��A��B�����㶼��Բ P �ϣ�
������֪ B��-3��0�����������ϴ���һ�� M ʹ��ABM �����Ϊ 15����� M �����ꣻ
�����жϣ����� m ȡ�κ�������Բ P �Ƿ� y ����ij�����㣿���ǣ�����ö�������꣬�����ǣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
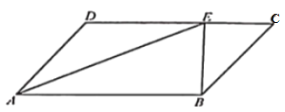
����Ŀ����ͼ����ƽ���ı���ABCD�У�AEƽ����DAB����֪CE=6��BE=8��DE=10.
��1����֤����BEC=90����
��2����cos��DAE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
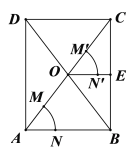
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�O�������²�����ͼ�����Ե�AΪԲ�ģ������ⳤΪ�뾶�������ֱ�AO��AB�ڵ�M��N�����Ե�OΪԲ�ģ���AM��Ϊ�뾶��������OC�ڵ�M'�����Ե�M'ΪԲ�ģ���MN��Ϊ�뾶�������ڡ�COB�ڲ���ǰ��Ļ��ڵ�N'���ܹ���N'������ON'��BC�ڵ�E����AB��8�����߶�OE�ij�Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y= ![]() +��1-2a��x��a��0��������˵��������ǣ�������
+��1-2a��x��a��0��������˵��������ǣ�������
A. ��![]() ʱ���ö��κ���ͼ��ĶԳ���Ϊy��
ʱ���ö��κ���ͼ��ĶԳ���Ϊy��
B. ��a��![]() ʱ���ö��κ���ͼ��ĶԳ�����y����Ҳ�
ʱ���ö��κ���ͼ��ĶԳ�����y����Ҳ�
C. �ö��κ�����ͼ��ĶԳ����Ϊx=1
D. ��x��2ʱ��y��ֵ��x��ֵ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �ڽ���
�ڽ���![]() ��
��![]() ��ֱ������
��ֱ������![]() ��
��![]() �ϣ�
�ϣ�![]() ������
������![]() ��
��![]() ������Ϊ
������Ϊ![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
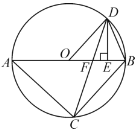
��1����֤��![]() ��
��
��2����֤��![]() ��
��
��3������![]() ����
����![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����ı���
�����ı���![]() ��������ú���
��������ú���![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com