
如图,AB为⊙O的直径,与弦CD相交于点E,且AC=2,AE= ,CE=1.求
,CE=1.求 的长度.
的长度.

科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:解答题
对于两个相似三角形,如果对应顶点沿边界按相同方向顺序环绕,那么称这两个三角形互为同相似,如图1, ∽
∽ ,则称
,则称 与
与 互为同相似;如果对应顶点沿边界按相反方向顺序环绕,那么称这两个三角形互为异相似,如图2,
互为同相似;如果对应顶点沿边界按相反方向顺序环绕,那么称这两个三角形互为异相似,如图2,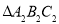 ∽
∽ ,则称
,则称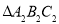 与
与 互为异相似.
互为异相似.

(1)在图3、图4和图5中,△ADE∽△ABC, △HXG∽△HGF,△OPQ∽△OMN,其中△ADE与△ABC互为 相似,△HXG与△HGF互为 相似,△OPQ与△OMN互为 相似;
(2)在锐角△ABC中,?A<?B<?C,点P为AC边上一定点(不与点A,C重合),过这个定点P画直线截△ABC,使截得的一个三角形与△ABC互为异相似,符合条件的直线有_____条.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3, AB=6,那么AD的值为( )

A. B.
B.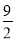 C.
C.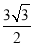 D.
D.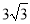
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知二次函数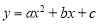 (
(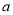 为常数,且
为常数,且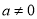 )的图象过点A(0,1),B(1,-2)和点C(-1,6).
)的图象过点A(0,1),B(1,-2)和点C(-1,6).
(1)求二次函数表达式;
(2)若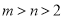 ,比较
,比较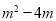 与
与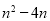 的大小;
的大小;
(3)将抛物线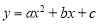 平移,平移后图象的顶点为
平移,平移后图象的顶点为 ,若平移后的抛物线与直线
,若平移后的抛物线与直线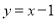 有且只有一个公共点,请用含
有且只有一个公共点,请用含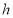 的代数式表示
的代数式表示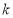 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,在平行四边形ABCD中,点E是边AD的中点,连接EC交对角线BD于点F,则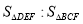 等于 ( )
等于 ( )

A.1:2 B.1:4 C.1:9 D.4:9
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市大兴区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,求DC的长
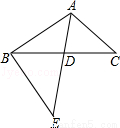
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市昌平区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知:如图,一次函数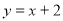 的图象与反比例函数
的图象与反比例函数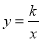 的图象交于A、B两点,且点A的坐标为(1,m).
的图象交于A、B两点,且点A的坐标为(1,m).
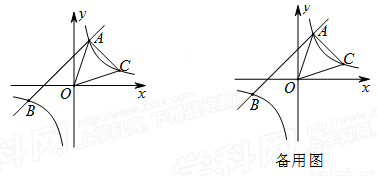
(1)求反比例函数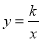 的表达式;
的表达式;
(2)点C(n,1)在反比例函数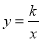 的图象上,求△AOC的面积;
的图象上,求△AOC的面积;
(3)在x轴上找出点P,使△ABP是以AB为斜边的直角三角形,请直接写出所有符合条件的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com