
| 3 |
| 3 |
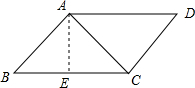 解:过点A作AE⊥BC于点E,
解:过点A作AE⊥BC于点E,| 1 |
| 2 |
| 3 |
| 3 |
| 3 |


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
 某拱桥的横截面呈抛物线形,桥下水面宽为AB(单位:米).以水面宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系.抛物线解析式为y=-x2+4
某拱桥的横截面呈抛物线形,桥下水面宽为AB(单位:米).以水面宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系.抛物线解析式为y=-x2+4| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
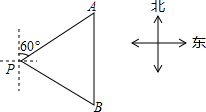 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行80海里后,到达B处,求此时轮船所在的B处相对于灯塔P的位置.(结果保留根号)
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行80海里后,到达B处,求此时轮船所在的B处相对于灯塔P的位置.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:
 在菱形OABC中,A点在反比例函数y=
在菱形OABC中,A点在反比例函数y=| k |
| x |
| 2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
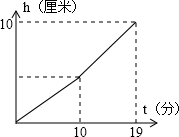 一个容器由上下竖直放置的两个圆柱体A,B连接而成.向该容器内匀速注水,容器内水面的高度h(厘米)与注水时间t(分)的函数关系如图所示.若上面A圆柱体的底面积是300厘米2,下面圆柱体B的底面积是500厘米2.则每分钟向容器内注水
一个容器由上下竖直放置的两个圆柱体A,B连接而成.向该容器内匀速注水,容器内水面的高度h(厘米)与注水时间t(分)的函数关系如图所示.若上面A圆柱体的底面积是300厘米2,下面圆柱体B的底面积是500厘米2.则每分钟向容器内注水查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com