
【题目】如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知∠B=30°,∠C=45°. 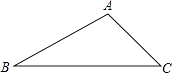
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据: ![]() ≈1.7,
≈1.7, ![]() ≈1.4)
≈1.4)
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】根据图形填空:

(1)若直线ED,BC被直线AB所截,则∠1和__________是同位角.
(2)若直线ED,BC被直线AF所截,则∠3和__________是内错角.
(3)∠1和∠3是直线AB,AF被直线__________所截构成的__________角.
(4)∠2和∠4是直线__________,__________被直线BC所截构成的__________角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,BD、CE分别是边AC、AB上的高,点M是BC的中点,且MN⊥DE,垂足为点N
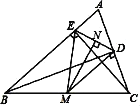
⑴求证:ME=MD;
⑵若BC=20cm,ED=12cm,求MN的长
⑶如果BD平分∠ABC,求证:AC=4EN.
查看答案和解析>>
科目:初中数学 来源: 题型:
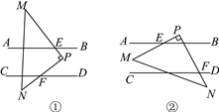
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,求出∠PFD与∠AEM的数量关系;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=15°,∠PEB=30°,求∠N的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一个角的补角比它的余角的 3 倍大 30°,求这个角的度数;
(2)如图,点 C、D在线段 AB上, D是线段 AB的中点, AC ![]() AD , AB6,求线段 CD的长.
AD , AB6,求线段 CD的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
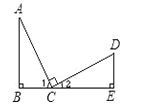
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读以下内容:
已知实数x,y满足x+y=2,且![]() 求k的值.
求k的值.
三位同学分别提出了以下三种不同的解题思路:
甲同学:先解关于x,y的方程组![]() ,再求k的值.
,再求k的值.
乙同学:先将方程组中的两个方程相加,再求k的值.
丙同学:先解方程组![]() ,再求k的值.
,再求k的值.
(2)你最欣赏(1)中的哪种思路?先根据你所选的思路解答此题,再对你选择的思路进行简要评价.
(评价参考建议:基于观察到题目的什么特征设计的相应思路,如何操作才能实现这些思路、运算的简洁性,以及你依此可以总结什么解题策略等等)
请先在以下相应方框内打勾,再解答相应题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,
轴上,![]() 轴,
轴,![]() 轴.点
轴.点![]() 从点
从点![]() 出发,以1个单位长度/秒的速度,沿五边形
出发,以1个单位长度/秒的速度,沿五边形![]() 的边顺时针匀速运动一周,若顺次连接
的边顺时针匀速运动一周,若顺次连接![]() ,
,![]() ,
,![]() 三点所围成的三角形的面积为
三点所围成的三角形的面积为![]() ,点
,点![]() 运动的时间为
运动的时间为![]() 秒,已知
秒,已知![]() 与
与![]() 之间的函数关系如图②中折线
之间的函数关系如图②中折线![]() 所示.
所示.
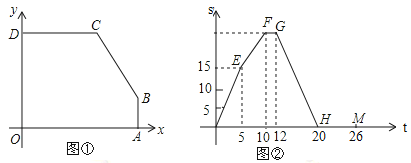
(1)图①中点![]() 的坐标为 ;点
的坐标为 ;点![]() 的坐标为 ;
的坐标为 ;
(2)求图②中![]() 所在直线的解析式;
所在直线的解析式;
(3)是否存在点![]() ,使
,使![]() 的面积为五边形
的面积为五边形![]() 的面积的
的面积的![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com