
����Ŀ����1���Ķ��������ݣ�
��֪ʵ��x��y����x+y=2����![]() ��k��ֵ��
��k��ֵ��
��λͬѧ�ֱ�������������ֲ�ͬ�Ľ���˼·��
��ͬѧ���Ƚ����x��y�ķ�����![]() ������k��ֵ��
������k��ֵ��
��ͬѧ���Ƚ��������е�����������ӣ�����k��ֵ��
��ͬѧ���Ƚⷽ����![]() ������k��ֵ��
������k��ֵ��
��2���������ͣ�1���е�����˼·���ȸ�������ѡ��˼·�����⣬�ٶ���ѡ���˼·���м�Ҫ���ۣ�
�����۲ο����飺���ڹ۲쵽��Ŀ��ʲô������Ƶ���Ӧ˼·����β�������ʵ����Щ˼·������ļ���ԣ��Լ������˿����ܽ�ʲô������Եȵȣ�
������������Ӧ�����ڴ��ٽ����Ӧ��Ŀ��
���𰸡��������ͣ�1���е���ͬѧ�Ľ���˼·��k=![]() ,���ۼ�����.
,���ۼ�����.
�����������������ѡ����ͬѧ�Ľ���˼·����+�ڵó�5x+5y=7k+4�����x+y=![]() =2����������𰸣�
=2����������𰸣�
���������
�������ͣ�1���е���ͬѧ�Ľ���˼·��
![]() ��
��
��+�ڵã�5x+5y=7k+4��
x+y=![]() ��
��
��x+y=2��
��![]() =2��
=2��
��ã�k=![]() ��
��
���ۣ���ͬѧ��ֱ�Ӹ��ݷ�����Ľ�ĸ����Ƚⷽ���飬�õ��ú�k��ʽ�ӱ�ʾx��y�ı���ʽ���ٴ���x+y=2�õ�����k�ķ��̣�û�о�������Ĺ۲��˼�����ⷨ�ȽϷ�������������
��ͬѧ�۲쵽�˷�������δ֪��x��y��ϵ�����Լ���x+y=2�е�ϵ���������ϵ���������������㣬���Ҳ������x��y��ֵ���ܽ�����⣬˼·�Ƚ���������С��
��ͬѧ������������Ϊһ�����壬���ɹ���x��y��k����Ԫһ�η����飬����ѡ���Ƚ�����ֻ��������δ֪��x��y�Ķ�Ԫһ�η����飬��Լ�������С����������ͬѧ�ļ�ࡢ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1=��2����һ����ʹ��ABD�ա�ACD�������ǣ� ��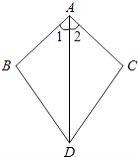
A.AB=AC
B.BD=CD
C.��B=��C
D.��BDA=��CDA
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ף�����֧��ӵ�������ȣ�ƽ�����߶���1.72�ף�����ֱ���S��2=0.35��S��2=0.27����ס������������߽���������ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABб����һ��ֱ��ǽ�ϣ����ӵĵ�A��ǽ��O�ľ���AOΪ2�ף����ӵĶ���B������ľ���BOΪ6�ף��ֽ����ӵĵ�A�����ƶ���A�䣬ʹ���ӵĵ�A�䵽ǽ��O�ľ���A��O����3�ף�ͬʱ���ӵĶ���B�½���B�䣮�����Ӷ����»��ľ���BB�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֽ���ʽm��ma2�Ľ���ǣ�������
A.m��1+a����1��a��
B.m��1+a��2
C.mm��1��a��2
D.��1��a����1+a��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m3��9m�ֽ���ʽ��ȷ���ǣ�������
A.m��m2��9��
B.m��m��3��2
C.m��m+3����m��3��
D.m��m+9����m��9��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ǽ�������ǣ�������
A. ��ֱ��ƽ�У�ͬλ�����B. ��a=b����a��3=b��3
C. ���е�ֱ�Ƕ�����ȵ�D. ��ȵĽ��ǶԶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������У�����֤����ABC�ա�DCB���ǣ� ��
A.AB=CD��AC=BD
B.AB=CD����ABC=��BCD
C.��ABC=��DCB����A=��D
D.AB=CD����A=��D
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com