
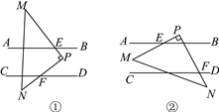
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,求出∠PFD与∠AEM的数量关系;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=15°,∠PEB=30°,求∠N的度数.
【答案】(1)∠PFD+∠AEM=90°;(2)见解析;(3)∠N=45°.
【解析】
(1)如图,由平行线的性质得出∠PFD=∠NPH,∠AEM=∠HPM,即可得出结果;
(2)设PN交AB于点G,由平行线的性质得出∠PFD=∠PGB,再由三角形的外角等于与它不相邻的两个内角的和即可得出结果;
(3)由三角形的外角等于与它不相邻的两个内角的和求出∠PFD=90°+∠PEB=120°,再由平行线的性质得出∠NFO=120°,然后由三角形的内角和定理即可得出结果.
解:(1)如图,过点P作PH∥AB.
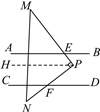
∵AB∥CD,
∴PH∥CD,
∴∠PFD=∠NPH,∠AEM=∠HPM.
∵∠MPN=90°,
∴∠NPH+∠HPM=90°,
∴∠PFD+∠AEM=90°.
(2)证明:设PN交AB于点G.
∵AB∥CD,
∴∠PFD=∠PGB.
∵∠PGB-∠PEB=90°,∠PEB=∠AEM,
∴∠PFD-∠AEM=90°.
(3)由(2)得,∠PFD=90°+∠PEB=120°,
∴∠NFO=120°,
∴∠N=180°-∠DON-∠NFO=45°.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,BE平分∠ABD,DE平分∠BDC,且BE与DE相交于点E,求证∠E=90° 证明:∵AB∥CD()
∴∠ABD+∠BDC=180°()
∵BE平分∠ABD()
∴∠EBD= ![]() ()
()
又∵DE平分∠BDC
∴∠BDE= ![]() ()
()
∴∠EBD+∠EDB= ![]() ∠ABD+
∠ABD+ ![]() ∠BDC()
∠BDC()
= ![]() (∠ABD+∠BDC)=90°
(∠ABD+∠BDC)=90°
∴∠E=90°.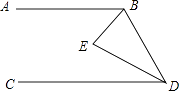
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2﹣(2m﹣5)x+m﹣2的图象与x轴有两个公共点.
(1)求m的取值范围,并写出当m取范围内最大整数时函数的解析式;
(2)题(1)中求得的函数记为C1 ,
①当n≤x≤﹣1时,y的取值范围是1≤y≤﹣3n,求n的值;
②函数C2:y=m(x﹣h)2+k的图象由函数C1的图象平移得到,其顶点P落在以原点为圆心,半径为 ![]() 的圆内或圆上,设函数C1的图象顶点为M,求点P与点M距离最大时函数C2的解析式.
的圆内或圆上,设函数C1的图象顶点为M,求点P与点M距离最大时函数C2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB 的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.当一个点停止运动时时,另一个点也随之停止运动.设运动时间为t.
(1)用含有t的代数式表示CP.
(2)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知∠B=30°,∠C=45°. 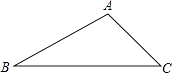
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据: ![]() ≈1.7,
≈1.7, ![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一样),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com