
【题目】如图,AB∥CD,BE平分∠ABD,DE平分∠BDC,且BE与DE相交于点E,求证∠E=90° 证明:∵AB∥CD()
∴∠ABD+∠BDC=180°()
∵BE平分∠ABD()
∴∠EBD= ![]() ()
()
又∵DE平分∠BDC
∴∠BDE= ![]() ()
()
∴∠EBD+∠EDB= ![]() ∠ABD+
∠ABD+ ![]() ∠BDC()
∠BDC()
= ![]() (∠ABD+∠BDC)=90°
(∠ABD+∠BDC)=90°
∴∠E=90°.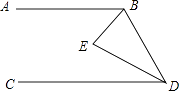
【答案】已知;两直线平行,同旁内角互补;已知;∠ABD;角平分线的定义;∠CDB;角平分线的定义;等式的性质
【解析】证明:∵AB∥CD(已知) ∴∠ABD+∠BDC=180°(两直线平行,同旁内角互补)
∵BE平分∠ABD(已知)
∴∠EBD= ![]() ∠ABD(角平分线的定义)
∠ABD(角平分线的定义)
又∵DE平分∠BDC
∴∠BDE= ![]() ∠CDB(角平分线的定义)
∠CDB(角平分线的定义)
∴∠EBD+∠EDB= ![]() ∠ABD+
∠ABD+ ![]() ∠BDC(等式的性质)
∠BDC(等式的性质)
= ![]() (∠ABD+∠BDC)=90°
(∠ABD+∠BDC)=90°
∴∠E=90°.
所以答案是:已知,两直线平行,同旁内角互补,已知,∠ABD,角平分线的定义,∠CDB,角平分线的定义,等式的性质
【考点精析】利用平行线的性质对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )
A.红红不是胜就是输,所以红红胜的概率为 ![]()
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为 ![]()
D.娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图形填空:

(1)若直线ED,BC被直线AB所截,则∠1和__________是同位角.
(2)若直线ED,BC被直线AF所截,则∠3和__________是内错角.
(3)∠1和∠3是直线AB,AF被直线__________所截构成的__________角.
(4)∠2和∠4是直线__________,__________被直线BC所截构成的__________角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )
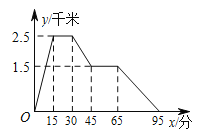
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为 ![]() ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( ) 
A.![]()
B.![]()
C.![]() ﹣
﹣ ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,BD、CE分别是边AC、AB上的高,点M是BC的中点,且MN⊥DE,垂足为点N
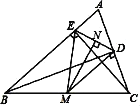
⑴求证:ME=MD;
⑵若BC=20cm,ED=12cm,求MN的长
⑶如果BD平分∠ABC,求证:AC=4EN.
查看答案和解析>>
科目:初中数学 来源: 题型:
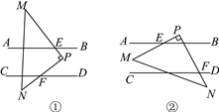
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,求出∠PFD与∠AEM的数量关系;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=15°,∠PEB=30°,求∠N的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读以下内容:
已知实数x,y满足x+y=2,且![]() 求k的值.
求k的值.
三位同学分别提出了以下三种不同的解题思路:
甲同学:先解关于x,y的方程组![]() ,再求k的值.
,再求k的值.
乙同学:先将方程组中的两个方程相加,再求k的值.
丙同学:先解方程组![]() ,再求k的值.
,再求k的值.
(2)你最欣赏(1)中的哪种思路?先根据你所选的思路解答此题,再对你选择的思路进行简要评价.
(评价参考建议:基于观察到题目的什么特征设计的相应思路,如何操作才能实现这些思路、运算的简洁性,以及你依此可以总结什么解题策略等等)
请先在以下相应方框内打勾,再解答相应题目.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com