
【题目】已知⊙![]() 是△
是△![]() 的外接圆,
的外接圆,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是
是![]() 延长线上的一点,
延长线上的一点,![]() 交
交![]() 的延长线于
的延长线于![]() ,交⊙
,交⊙![]() 于
于![]() ,
,![]() 于
于![]() ,点
,点![]() 是弧
是弧![]() 的中点.
的中点.
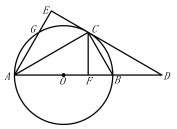
⑴求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
⑵若![]() 是一元二次方程
是一元二次方程![]() 的两根,求
的两根,求![]() 和
和![]() 的长.
的长.
【答案】(1)见解析;(2)CE=![]() ,AG=4
,AG=4
【解析】
(1)连接![]() ,由
,由![]() ,
,![]() ,得:
,得:![]() ,从而得:
,从而得:![]() ∥
∥![]() ,进而得到:
,进而得到:![]() ,即可得证;
,即可得证;
(2)易得:![]() ,由CAF~BCF,得:
,由CAF~BCF,得:![]() ,进而得:
,进而得:![]() ,进而求得CE的长,由
,进而求得CE的长,由![]() △
△![]() ≌
≌![]() △
△![]() (HL),得:
(HL),得:![]() ,由
,由![]() △
△![]() ≌
≌![]() △
△![]() (HL),得
(HL),得![]() ,进而求出AG的长.
,进而求出AG的长.
⑴.证明:连接![]() ,如图1,
,如图1,
∵![]() ,
,
∴![]() ,
,
∵点![]() 是弧
是弧![]() 的中点,即
的中点,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ∥
∥![]() ,
,
∴ ![]() ,
,
∵![]() ,
,
∴![]() , 即
, 即![]() ,
,
又∵![]() 是⊙
是⊙![]() 的半径,
的半径,
∴![]() 是⊙
是⊙![]() 的切线.
的切线.
⑵解一元二次方程![]() 的两根为:
的两根为:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是⊙
是⊙![]() 的直径,
的直径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵∠CAF+∠ACF=90°,∠ACF+∠BCF=90°,
∴∠CAF=∠BCF,
∴CAF~BCF,
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,
∵![]() ,且
,且![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() △
△![]() ≌
≌![]() △
△![]() (HL),
(HL),
∴![]() ,
,
连接![]() ,如图2,
,如图2,
∵点![]() 是弧
是弧![]() 的中点,即
的中点,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() △
△![]() ≌
≌![]() △
△![]() (HL),
(HL),
∴![]() ,
,
∴![]() .
.
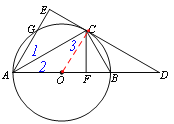

图1 图2


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】某地区的居民用电,按照高峰时段和空闲时段规定了不同的单价.某户5月份高峰时段用电量是空闲时段用电量2倍,6月份高峰时段用电量比5月份高峰时段用电量少50%,结果6月份的用电量和5月份的用电量相等,但6月份的电费却比5月份的电费少25%,求该地区空闲时段民用电的单价比高峰时段的用电单价低的百分率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,DC为⊙O的切线,DE⊥AB,垂足为点E,交⊙O于点F,弦AC交DE于点P,连接CF.
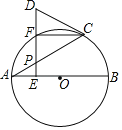
(1)求证:∠DPC=∠PCD;
(2)若AP=2,填空:
①当∠CAB= 时,四边形OBCF是菱形;
②当AC=2AE时,OB= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一动点(点
边上一动点(点![]() 与点
与点![]() 不重合),联结
不重合),联结![]() ,过点
,过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() .
.
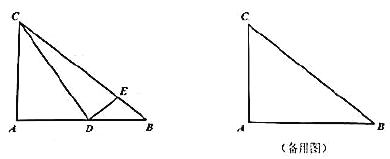
(1)如图,当![]() 时,求
时,求![]() 的长;
的长;
(2)设![]() ,求
,求![]() 关于
关于![]() 的函数解析式并写出函数定义域;
的函数解析式并写出函数定义域;
(3)把![]() 沿直线
沿直线![]() 翻折得
翻折得![]() ,联结
,联结![]() ,当
,当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,直径
中,直径![]() 垂直于不过圆心
垂直于不过圆心![]() 的弦
的弦![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 为
为![]() 上一动点,设线段
上一动点,设线段![]() 的长为
的长为![]() .
.
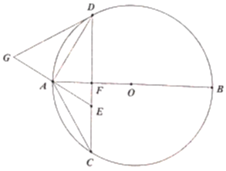
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)设![]() 半径为
半径为![]() ,若点
,若点![]() 为
为![]() 中点,求
中点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,连接
上一点,连接![]()
(1)如图1,若![]() ,
,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 与
与![]() 垂直,求证:
垂直,求证:![]()
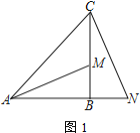
(2)过点![]() 作
作![]() ,
,![]() 为垂足,连接
为垂足,连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
①如图2,若![]() ,求证:
,求证:![]()
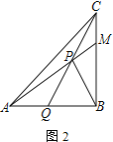
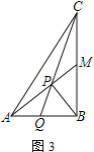
②如图3,若![]() 是
是![]() 的中点,直接写出
的中点,直接写出![]() 的值(用含
的值(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)的对称轴为x=-1,与x轴的一个交点为(2,0).若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com