
【题目】如图1,在平面直角坐标系中,将ABCD放置在第一象限,且AB∥x轴.直线y=﹣x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么AD的长为 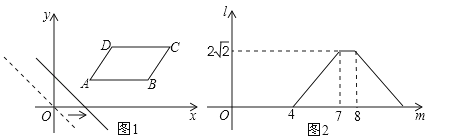
【答案】![]()
【解析】解:
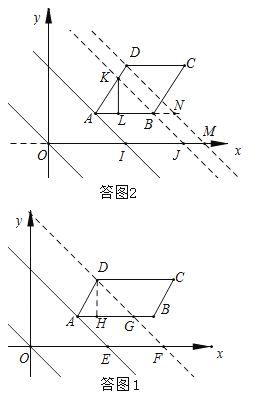
①先经过点D,即AB>3,如答图1:
设直线过点A时交x轴于点E,过点D交AB于点G,交x轴于点F,作DH⊥AB,
由图可知:OE=4,OF=7,DG=2![]() ,
,
∴EF=AG=OF﹣OE=3
∵直线y=﹣x
∴∠AGD=∠EFD=45°
∴△HGD是等腰直角三角形
∴DH=GH=![]() DG=
DG=![]() ×2
×2![]() =2
=2
∴AH=AG﹣GH=3﹣2=1
∴AD=![]()
②先经过点B,即AB=3,如答图2:
设直线过点A时交x轴于点I,过点B时交AD于点K、x轴于点J,过点D时,交AB延长线于点N、x轴于点M,并过K点作KL⊥AB,
由图可知:OI=4,OJ=7,KB=2![]() , OM=8,
, OM=8,
∴IJ=AB=3,IM=AN=4,
由直线y=﹣x,易得△KLB是等腰直角三角形,
∴KL=BL=![]() KB=
KB=![]() ×2
×2![]() =2,
=2,
∴AL=1,
∴AK=![]()
∵△ABK∽△AND,
∴![]() ,
,
即![]()
即AD=![]() .
. 
根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7﹣8这段时,l的长度是不变的,可以得出直线是正好经过且在两条平行线 之间的,故此时需要分两种情况:①先经过点D,即AB>3,利用直线的性质得到△HGD是等腰直角三角形,从而求出DH、AH的值,再利用勾股定理解得 AD;②先经过点B,即AB=3,利用等腰直角三角形△KLB的性质得到AK的值,然后利用△ABK∽△AND,可得到AD的值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts. 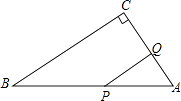
(1)用含t的式子表示线段AP、AQ的长;
(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?
(3)当t为何值时,PQ∥BC?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业2018年初获利润300万元,到2020年初计划利润达到507万元,求这两年的年利润的平均增长率,设企业这两年的年利润平均增长率为x,则可列方程为( )
A. 300(1+x)2=507B. 300(1﹣x)2=507
C. 300(1+2x)=507D. 300(1+x2)=507
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.

(1)m= %,这次共抽取 名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有1500名学生,请你估计该校骑自行车上学的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A,B两种花草,第一次分别购进A,B两种花草30棵和15棵,共花费675元;第二次分别购进A,B两种花草12棵和5棵.两次共花费940元(两次购进的A,B两种花草价格均分别相同).
(1)A,B两种花草每棵的价格分别是多少元?
(2)若购买A,B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按括号内的要求,用四舍五入法对下列各数取近似数:
(1)5.045≈_____(精确到百分位);
(2)23.04≈_____(精确到0.1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com