
����Ŀ��ijС��Ϊ���̻��������ƻ������ι���A��B���ֻ��ݣ���һ�ηֱ�A��B���ֻ���30�ú�15�ã�������675Ԫ���ڶ��ηֱ�A��B���ֻ���12�ú�5�ã����ι�����940Ԫ�����ι�����A��B���ֻ��ݼ۸���ֱ���ͬ����
��1��A��B���ֻ���ÿ�õļ۸�ֱ��Ƕ���Ԫ��
��2��������A��B���ֻ��ݹ�31�ã���B�ֻ��ݵ���������A�ֻ��ݵ�������2�����������һ�ַ�����ʡ�ķ�����������÷���������ã�
���𰸡�
��1���⣺��A�ֻ���ÿ�õļ۸�xԪ��B�ֻ���ÿ�õļ۸�yԪ����������ã�
![]() ��
��
��ã� ![]() ��
��
��A�ֻ���ÿ�õļ۸���20Ԫ��B�ֻ���ÿ�õļ۸���5Ԫ��
��2���⣺��A�ֻ��ݵ�����Ϊm�꣬��B�ֻ��ݵ�����Ϊ��31��m���꣬
��B�ֻ��ݵ���������A�ֻ��ݵ�������2����
��31��m��2m��
��ã�m�� ![]() ��
��
��m����������
��m��Сֵ=11��
�蹺�������ܷ���ΪW=20m+5��31��m��=15m+155��
��k��0��
��W��x�ļ�С����С��
��m=11ʱ��W��Сֵ=15��11+155=320��Ԫ����
�𣺹���A�ֻ��ݵ�����Ϊ11�ꡢB��20�꣬������ʡ����ʡ������320Ԫ��
����������1����A�ֻ���ÿ�õļ۸�xԪ��B�ֻ���ÿ�õļ۸�yԪ�����ݵ�һ�ηֱ�A��B���ֻ���30�ú�15�ã�������940Ԫ���ڶ��ηֱ�A��B���ֻ���12�ú�5�ã����ι�����675Ԫ���г������飬���ɽ�𣮣�2����A�ֻ��ݵ�����Ϊm�꣬��B�ֻ��ݵ�����Ϊ��31��m���꣬����B�ֻ��ݵ���������A�ֻ��ݵ�������2�����ó�m�ķ�Χ�����ܷ���ΪWԪ�������ܷ���=���ֻ��ݵķ���֮�ͽ���������ϵʽ����һ�κ��������ʾͿ���������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������2��3��ʾ��������
A. ��2��3 B. ����2��+����2��+����2��
C. ��2��2��2 D. ����2��������2��������2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���ABCD�����ڵ�һ���ޣ���AB��x�ᣮֱ��y=��x��ԭ�������x��������ƽ�ƣ���ƽ�ƹ�����ֱ�߱�ƽ���ı��νصõ��߶γ���l��ֱ����x����ƽ�Ƶľ���m�ĺ���ͼ����ͼ2��ʾ����ôAD�ij�Ϊ 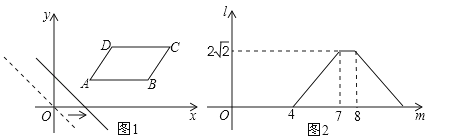
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�ֲ�Ʒ�����Ƚ����ϼ��ȴﵽ60�����ٽ��в�������ò����¶�Ϊy���������Ӽ��ȿ�ʼ�����ʱ��Ϊx�����ӣ������˽⣬��ò��ϼ���ʱ���¶�y��ʱ��x��һ�κ�����ϵ��ֹͣ���Ƚ��в���ʱ���¶�y��ʱ��x�ɷ�������ϵ����ͼ������֪�ò����ڲ����ӹ�ǰ���¶�Ϊ15��������5���Ӻ��¶ȴﵽ60����

(1)����������ϼ���ʱ��y��x�ĺ�����ϵʽ��
(2)�����ֹͣ���Ƚ��в���ʱ��y��x�ĺ�����ϵʽ��
(3)�����ݹ���Ҫ�����ϵ��¶ȵ���15��ʱ����ֹͣ��������ô����ʱ���Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������ͼ�������ݣ�������и�С�⣮ 
��1����m��n=1��m��2n=��2���ֱ���m��n��ֵ��
��2����m����m��2��0����3m������8����0����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����D�ǡ�ABC�ı�AB���е㣬�ı���BCED��ƽ���ı��Σ�
��1����֤���ı���ADCE��ƽ���ı��Σ�
��2������ABC����ʲô����ʱ��ƽ���ı���ADCE�Ǿ��Σ�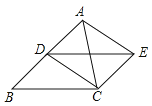
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ж���ȷ���ǣ�������
A. һ��Ա�ƽ�У���һ��Ա���ȵ��ı���һ����ƽ���ı���
B. �����Խ�����ƽ�ֵ��ı���һ����ƽ���ı���
C. �����ڽǷֱ����ı���һ����ƽ���ı���
D. �����Խ�����ȵ��ı���һ����ƽ���ı���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com