
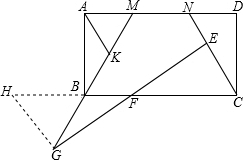
 如图,在矩形ABCD中,点M、N在线段AD上,∠MBC=∠NCB=60°,点E、F分别为线段CN、BC上的点,连接EF并延长,交MB的延长线于点G,EF=FG.
如图,在矩形ABCD中,点M、N在线段AD上,∠MBC=∠NCB=60°,点E、F分别为线段CN、BC上的点,连接EF并延长,交MB的延长线于点G,EF=FG.| 1 |
| 2 |
| BM2-AM2 |
| 42-22 |
| 3 |
| CD | ||
|
2
| ||
|
| 3 |
| 3 |
|
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 月销量x(件) | 1500 | 2000 |
| 销售价格y(元/件) | 185 | 180 |
| 1 |
| 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、通常加热到100℃时,水沸腾 |
| B、篮球队员在罚球线上投篮一次,未投中 |
| C、度量三角形内角和,结果是360° |
| D、掷一个质地均匀的正方体骰子,向上的一面出现的点数大于0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
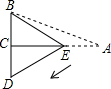 如图,在三角形纸片ABC中,∠BCA=90°,∠BAC=30°,AC=3
如图,在三角形纸片ABC中,∠BCA=90°,∠BAC=30°,AC=3| 3 |
| A、2 | ||
| B、3 | ||
C、2
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 月份x | 1月 | 2月 | 3月 | 4月 | 5月 |
| 销售量P(千克) | 70000 | 65000 | 60000 | 55000 | 50000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com