练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
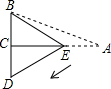
    如图，在三角形纸片ABC中，∠BCA=90°，∠BAC=30°，AC=3
    		3
    ，在AC上取一点E，以BE为折痕进行折叠，使得AB的一部分与BC重合，点A与点D对应，则线段DE的长度为（　　）
    A、2
    B、3
    C、2
    		3
    D、
    		3
    考点：翻折变换（折叠问题）
    专题：
    分析：在Rt△ABC中求出AB=6，BC=3，根据折叠的性质可得BD=BA=6，∠D=∠A=30°，在Rt△DCE中可求出DE．
    解答：解：在Rt△ABC中，∵∠BAC=30°，AC=3
    		3
    ，
    ∴AB=6，BC=3，
    由折叠的性质可得：BD=BA=6，∠D=∠A=30°，
    ∴CD=BD-BC=3，
    ∴DE=
    CD
    cos∠D
    =
    3
    		3
    2
    =2
    		3
    ．
    故选C．
    点评：本题考查了翻折变换及解直角三角形的知识，注意掌握翻折前后对应边相等、对应角相等，难度一般．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

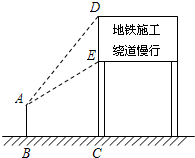    某市地铁工程正在加快建设，为了缓解市区内一些主要路段交通拥挤的现状，交警大队在一些主要路口设立了交通路况指示牌，如图所示，小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和32°．求路况指示牌DE的高度．（精确到0.01米）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知数轴上点A、B、C所表示的数分别是-2，+4，x．
    （1）请在数轴上标出A、B两点；

    （2）若AC=1，求x的值；
    （3）求线段AB的中点D所表示的数；
    （4）若x＜0，用x的代数式表示线段AC与线段BC的长度和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在矩形ABCD中，点M、N在线段AD上，∠MBC=∠NCB=60°，点E、F分别为线段CN、BC上的点，连接EF并延长，交MB的延长线于点G，EF=FG．
    （1）点K为线BM的中点，若线段AK=2，MN=3，求矩形ABCD的面积；
     （2）求证：MB=NE+BG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知△ABC中，AB=AC，D是BC上一点，且AD=DB，DC=CA，则∠BAC=
     
    °．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在△ABC中，∠A是钝角，H是垂心，AH=BC，则∠BHC=（　　）
    A、30°B、45°
    C、60°D、75°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    骨牌的形状有三种：边长为1的等边三角形，由两个边长为1的等边三角形形成的菱形和由3个边长为1的等边三角形所拼成的梯形．一副骨牌有222块菱形，333块等边三角形，444块梯形．是否能用这些骨牌 拼成一个周长为888的多边形．（在拼接时，骨牌与骨牌之间不能留有空隙）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，∠ABC=90°，BA=BC．点D是AB的中点，连接CD，过点B作BG丄CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G，连接DF．给出以下四个结论：①
    AG
    AB
    =
    FG
    FB
    ；②点F是GE的中点；③AF=
    		2
    3
    AB；④S△ABF=S△ACD，其中正确的结论序号是（　　）
    A、①②B、①③C、②③D、①④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    商城义乌江的两岸绿树葱茏、生机勃勃，成为我市一道亮丽的风景．如图，从义乌江的南岸C点测得两处风景A、B两点的视角∠ECA和∠ACB分别为30°和105°，测得BC=100
    		6
    米，假设南岸EF与北岸AB互相平行，求义乌江的宽度和A、B两处风景之间的距离．（精确到0.01米）（参考数据：
    		2
    ≈1.414，
    		3
    ≈1.732，
    		5
    ≈2.236）

    查看答案和解析>>

    同步练习册答案