
 商城义乌江的两岸绿树葱茏、生机勃勃,成为我市一道亮丽的风景.如图,从义乌江的南岸C点测得两处风景A、B两点的视角∠ECA和∠ACB分别为30°和105°,测得BC=100
商城义乌江的两岸绿树葱茏、生机勃勃,成为我市一道亮丽的风景.如图,从义乌江的南岸C点测得两处风景A、B两点的视角∠ECA和∠ACB分别为30°和105°,测得BC=100| 6 |
| 2 |
| 3 |
| 5 |
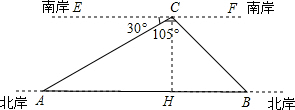 解:∵EF∥AB,∠ECA=30°,
解:∵EF∥AB,∠ECA=30°,| 6 |
| 3 |
| 3 |
| 3 |
| CH |
| tan30° |
100
| ||||
|


科目:初中数学 来源: 题型:
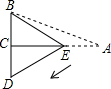 如图,在三角形纸片ABC中,∠BCA=90°,∠BAC=30°,AC=3
如图,在三角形纸片ABC中,∠BCA=90°,∠BAC=30°,AC=3| 3 |
| A、2 | ||
| B、3 | ||
C、2
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 现有一张演唱会的票,小明和小亮两人都想去.于是两想了个办法.用如图所示的两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成3等分,每份分别标有1,3,6这三个数字;转盘B被均匀地分成4等分,每份分别标有2,4,5,7这四个数字.①同时自由转动转盘A和B;②转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积为偶数,小明去,否则小亮去.这个方法公平吗?请你说明理由.若不公平,请你帮忙修改一个公平的规则.
现有一张演唱会的票,小明和小亮两人都想去.于是两想了个办法.用如图所示的两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成3等分,每份分别标有1,3,6这三个数字;转盘B被均匀地分成4等分,每份分别标有2,4,5,7这四个数字.①同时自由转动转盘A和B;②转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积为偶数,小明去,否则小亮去.这个方法公平吗?请你说明理由.若不公平,请你帮忙修改一个公平的规则.查看答案和解析>>
科目:初中数学 来源: 题型:
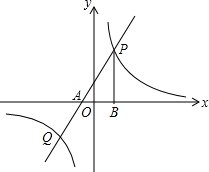 如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=
如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=| k |
| x |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
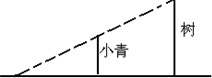 一天,小青在校园内发现:旁边一颗树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图所示).如果小青的身高为1.60米,由此可推断出树高是
一天,小青在校园内发现:旁边一颗树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图所示).如果小青的身高为1.60米,由此可推断出树高是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com