
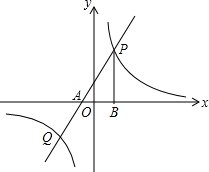
 如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=
如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=| k |
| x |
| 3 |
| 2 |
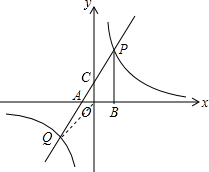 解:(1)∵A(-2,0),B(4,0),
解:(1)∵A(-2,0),B(4,0),| 3 |
| 2 |
| BP |
| 6 |
| 3 |
| 2 |
| k |
| x |
| 36 |
| x |
|
|
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
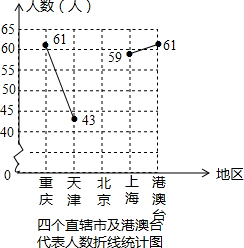 第十二届全国人大代表选举的基本原则是:城乡同比选举,实现人人平等、地区平等、民族平等.据新华网2月28日公布,全国5个少数民族自治区的人大代表如下:
第十二届全国人大代表选举的基本原则是:城乡同比选举,实现人人平等、地区平等、民族平等.据新华网2月28日公布,全国5个少数民族自治区的人大代表如下:| 选区 | 广西 | 西藏 | 新疆 | 宁夏 | 内蒙 |
| 人数(人) | 90 | 20 | 60 | 21 | 58 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 商城义乌江的两岸绿树葱茏、生机勃勃,成为我市一道亮丽的风景.如图,从义乌江的南岸C点测得两处风景A、B两点的视角∠ECA和∠ACB分别为30°和105°,测得BC=100
商城义乌江的两岸绿树葱茏、生机勃勃,成为我市一道亮丽的风景.如图,从义乌江的南岸C点测得两处风景A、B两点的视角∠ECA和∠ACB分别为30°和105°,测得BC=100| 6 |
| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在平面直角坐标系中,△ABC的位置如图所示,请解答下列问题:
在平面直角坐标系中,△ABC的位置如图所示,请解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com