Question

1．已知，梯形ABCD中，AD∥BC，∠ABC=60°且BC=8，梯形ABCD绕点A顺时针旋转α度后得到梯形AEFG，α为锐角．

（1）如图1，旋转过程中，若α=30°，则线段AB与线段EF是否有交点？是（填“是”或“否”），尝试并猜想，若线段AB与线段EF始终有交点时，α的取值范围是0°≤α≤60°．
（2）如图2，若B点落在线段EF上，F，G和D三点在同一直线上，则得到的四边形ABFG是平行四边形，你能证明吗？请写出理由．
（3）如图2中的平行四边形ABFG是菱形时，请求出此时梯形ABCD的面积．

Answer 1

分析 （1）如图1，画图可知，线段AB与线段EF有交点为H，当α=60°时，线段AB与线段EF的交点与点B重合，可得α的取值范围；
（2）如图3，连接GD，若B点落在线段EF上，则α=60°，由已知得AG∥BF，再证明AB∥GF即可；利用旋转的性质和已知梯形的性质得出∠ABE=∠F=60°，则AB∥FG，所以四边形ABFG是平行四边形；
（3）如图4，作梯形的高AN，根据等边三边形的性质求出上底，再利用三角函数值求高AN，代入面积公式计算即可．

解答 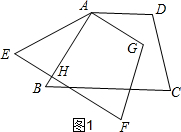解：（1）如图1，线段AB与线段EF有交点为H，
如图2，当α=60°时，线段AB与线段EF的交点与点B重合，所以若线段AB与线段EF始终有交点时，α的取值范围是0°≤α≤60°；
故答案为：是，0°≤α≤60°；
（2）如图3，连接GD，由已知得：F，G和D三点在同一直线上，
若B点落在线段EF上，则α=60°，
由旋转得：∠EAB=∠GAQ=60°，∠ABC=∠E=60°，AD=AG，
∴△AGD、△ABE都是等边三角形，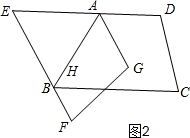
∴∠ADF=∠ABE=60°，
∵AD∥BC，
∴∠DAB+∠ABC=180°，
∴∠BAG=180°-60°-60°=60°，
∴E、A、D共线，
∵AD∥BC，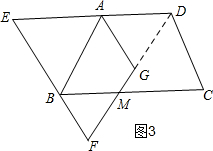
∴ED∥BC，
∴∠FBM=∠E=60°，∠BMF=∠ADF=60°，
∴∠F=60°，
∴∠ABE=∠F=60°，
∴AB∥FG，
∵AG∥EF，
∴四边形ABFG是平行四边形；
（3）当平行四边形ABFG是菱形时，如图4，点G在BC上，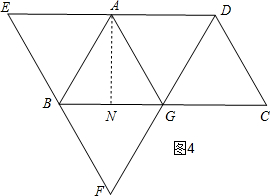
过A作AN⊥BC，垂足为N，
由（2）得：△AEB、△ADG、△ABG、△FBG是等边三角形，
∴EB=BF=BG=AD=AB=4，
在Rt△ABN中，sin∠ABC=$\frac{AN}{AB}$，
∴AN=sin60°×4=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$，
∴S_梯形ABCD=$\frac{1}{2}$（AD+BC）•AN=$\frac{1}{2}$×2$\sqrt{3}$（4+8）=12$\sqrt{3}$．

点评 本题是四边形的综合题，考查了梯形、平行四边形、等边三角形和菱形的性质和判定；同时又是旋转变换问题，熟练掌握旋转的性质，明确旋转前后的边和角对应相等，对应边的夹角就是旋转角；将等边三角形性质和三角函数相结合，求边的长度，利用面积公式求梯形的面积．