
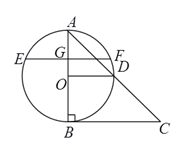
【题目】如图,在![]() 中,
中,![]() .以
.以![]() 为直径的⊙
为直径的⊙![]() 与
与![]() 相切于
相切于![]() ,交
,交![]() 于点
于点![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() ,过点作弦
,过点作弦![]() ,垂足为点
,垂足为点![]() .
.
(1)求证:①![]() ,②
,②![]() .
.
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(![]() )①证明见解析;②证明见解析;(
)①证明见解析;②证明见解析;(![]() )4
)4![]() .
.
【解析】(1) ①由切线的性质和垂径定理即可得证;(2)连接BD,由直径所对的圆周角为90°和等腰三角形的性质以及已知条件证明结论即可;(2)AB=2,则圆的直径为2,所以半径为1,即OB=OE=1,利用勾股定理求出CO的长,再通过证明△EOG∽△COB得到关于EG的比例式可求出EG的长,进而求出EF的长.
本题解析:
(![]() )①∵
)①∵![]() 为切线,切点为
为切线,切点为![]() ,
,![]() 为直径,∴
为直径,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
②连接![]() .
.
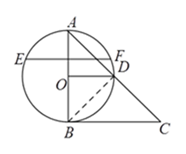
∵![]() 为直径,点
为直径,点![]() 在⊙
在⊙![]() 上,∴
上,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
(![]() )∵
)∵![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() ,
,![]() ,
,
∴(![]() )①∵
)①∵![]() 为切线,切点为
为切线,切点为![]() ,
,![]() 为直径,∴
为直径,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
②连接![]() .
.

∵![]() 为直径,点
为直径,点![]() 在⊙
在⊙![]() 上,∴
上,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
(![]() )∵
)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
.


科目:初中数学 来源: 题型:
【题目】下列能判定两个三角形全等的是( )
①三条边对应相等;②三个角对应相等;③两边和一个角对应相等;④两角和它们的夹边对应相等;⑤两角和一个角的对边对应相等.
A. ①②③ B. ①③⑤ C. ②③④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4) , 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为 t 秒.(直线y = kx+b平移时k不变)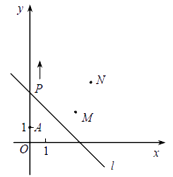
(1)当t=3时,求 l 的解析式;
(2)若点M,N位于l 的异侧,确定 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<![]() ).
).
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.
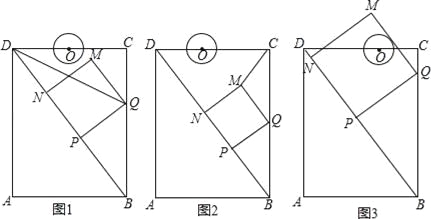
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[探究函数![]() 的图象与性质]
的图象与性质]
(1)函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)下列四个函数图象中函数![]() 的图象大致是 ;
的图象大致是 ;
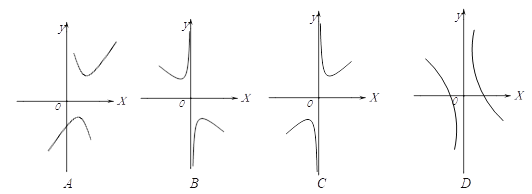
(3)对于函数![]() ,求当
,求当![]() 时,
时, ![]() 的取值范围.
的取值范围.
请将下列的求解过程补充完整.
解:∵![]()
∴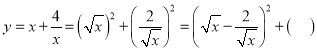
∵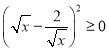
∴![]() .
.
[拓展运用]
(4)若函数![]() ,则
,则![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com