
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
【答案】(1)甲,乙两种套房每套提升费用分别为25万元,28万元.(2) 有三种方案分别是:方案一:甲种套房提升48套,乙种套房提升32套.方案二:甲种套房提升49套,乙种套房提升31套,方案三:甲种套房提升50套,乙种套房提升30套.第三种方案费用最少.(3) 当a=3时,三种方案的费用一样,都是2240万元.当a>3时,m=48时,费用W最小.当0<a<3时,, m=50时,W最小,费用最省.
【解析】
试题分析:(1)设甲种套房每套提升费用为x万元,根据题意建立方程求出其解即可;
(2)设甲种套房提升m套,那么乙种套房提升(80-m)套,根据条件建立不等式组求出其解就可以求出提升方案,再表示出总费用与m之间的函数关系式,根据一次函数的性质就可以求出结论;
(3)根据(2)表示出W与m之间的关系式,由一次函数的性质分类讨论就可以得出结论.
试题分析:(1)设甲种套房每套提升费用为x万元,依题意,
得![]() 解得:x=25
解得:x=25
经检验:x=25符合题意,x+3=28
答:甲,乙两种套房每套提升费用分别为25万元,28万元.
(2)设甲种套房提升m套,那么乙种套房提升(80-m)套,依题意,得
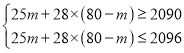
解得:48≤m≤50
即m=48或49或50,所以有三种方案分别是:
方案一:甲种套房提升48套,乙种套房提升32套.
方案二:甲种套房提升49套,乙种套房提升31套,
方案三:甲种套房提升50套,乙种套房提升30套.
设提升两种套房所需要的费用为W元.则
W=25m+28×(80-m)=-3m+2240,
∵k=-3<0,
∴W随m的增大而减小,
∴当m=50时,W最少=2090元,即第三种方案费用最少.
(3)在(2)的基础上有:W=(25+a)m+28×(80-m)=(a-3)m+2240
当a=3时,三种方案的费用一样,都是2240万元.
当a>3时,k=a-3>0,
∴W随m的增大而增大,
∴m=48时,费用W最小.
当0<a<3时,k=a-3<0,
∴W随m的增大而减小,
∴m=50时,W最小,费用最省.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法中错误的有( )个
①三角形的一个外角等于这个三角形的两个内角的和;
②直角三角形只有一条高;
③在同圆中任意两条直径都互相平分;
④n边形的内角和等于(n﹣2)360°.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在烟台市举办的“读好书、讲礼仪”活动中,东华学校积极行动,各班图书角的新书、好书不断增多,除学校购买外,还有师生捐献的图书,下面是七年级(1)班全体同学捐献图书的情况统计图:
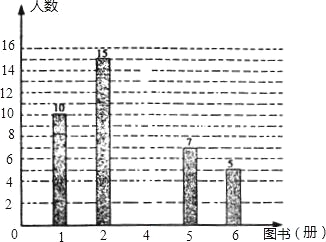
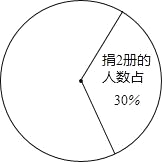
请你根据以上统计图中的信息,解答下列问题:
(1)该班有学生多少人?
(2)补全条形统计图;
(3)七(1)班全体同学所卷图书的中位数和众数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列选项中,给出的三条线段不能组成三角形的是 ( )
A. a+1,a+2,a+3B. 三边之比为2:3:4C. 30cm,8cm ,10cmD. 3k ,4k ,5k
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:

∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B=∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com