
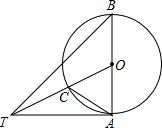
 如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
如图,AB是⊙O的直径,∠ABT=45°,AT=AB.分析 (1)根据等腰三角形的性质求得∠TAB=90°,得出TA⊥AB,从而证得AT是⊙O的切线;
(2)作CD⊥AT于D,设OA=x,则AT=2x,根据勾股定理得出OT=$\sqrt{5}$x,TC=($\sqrt{5}$-1)x,由CD⊥AT,TA⊥AB得出CD∥AB,根据平行线分线段成比例定理得出$\frac{CD}{OA}$=$\frac{TC}{OT}$=$\frac{TD}{TA}$,即$\frac{CD}{x}$=$\frac{(\sqrt{5}-1)x}{\sqrt{5}x}$=$\frac{TD}{2x}$,从而求得CD=(1-$\frac{\sqrt{5}}{5}$)x,AD=2x-2(1-$\frac{\sqrt{5}}{5}$)x=$\frac{2\sqrt{5}}{5}$x,然后解正切函数即可求得.
解答 解:(1)∵∠ABT=45°,AT=AB.
∴∠TAB=90°,
∴TA⊥AB,
∴AT是⊙O的切线;
(2)作CD⊥AT于D,
∵TA⊥AB,TA=AB=2OA,
设OA=x,则AT=2x,
∴OT=$\sqrt{5}$x,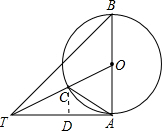
∴TC=($\sqrt{5}$-1)x,
∵CD⊥AT,TA⊥AB
∴CD∥AB,
∴$\frac{CD}{OA}$=$\frac{TC}{OT}$=$\frac{TD}{TA}$,即$\frac{CD}{x}$=$\frac{(\sqrt{5}-1)x}{\sqrt{5}x}$=$\frac{TD}{2x}$,
∴CD=(1-$\frac{\sqrt{5}}{5}$)x,TD=2(1-$\frac{\sqrt{5}}{5}$)x,
∴AD=2x-2(1-$\frac{\sqrt{5}}{5}$)x=$\frac{2\sqrt{5}}{5}$x,
∴tan∠TAC=$\frac{CD}{AD}$=$\frac{(1-\frac{\sqrt{5}}{5})x}{\frac{2\sqrt{5}}{5}x}$=$\frac{\sqrt{5}-1}{2}$.
或可以使用切割线定理:延长TO交圆与点G,连接AG.tan∠TAC=tan∠G=$\frac{CA}{GA}$=$\frac{CT}{TA}$=$\frac{(\sqrt{5}-1)x}{2x}$=$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了切线的判定,勾股定理的应用,平行线的判定和性质,解直角三角形等,作出辅助线构建直角三角形是解题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:填空题
 如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°.将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为2的平行四边形,则CD=2+$\sqrt{3}$或4+2$\sqrt{3}$.
如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°.将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为2的平行四边形,则CD=2+$\sqrt{3}$或4+2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.
如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
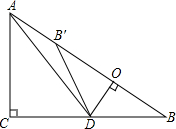 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
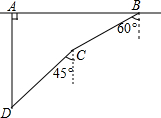 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 身高(cm) | 175 | 180 | 182 | 185 | 188 |
| 人数(个) | 1 | 5 | 4 | 2 | 1 |
| A. | 182,180 | B. | 180,180 | C. | 180,182 | D. | 188,182 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com