
 如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.
如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.分析 (1)作ME⊥x轴于E,则∠MEP=90°,先证出∠PME=∠CPO,再证明△MPE≌△PCO,得出ME=PO=t,EP=OC=4,求出OE,即可得出点M的坐标;
(2)连接AM,先证明四边形AEMF是正方形,得出∠MAE=45°=∠BOA,AM∥OB,证出四边形OAMN是平行四边形,即可得出MN=OA=4;
(3)先证明△PAD∽△PEM,得出比例式$\frac{AD}{ME}=\frac{AP}{EP}$,得出AD,求出BD,求出四边形BNDM的面积S是关于t的二次函数,即可得出结果.
解答 解:(1)作ME⊥x轴于E,如图1所示: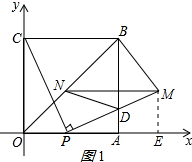
则∠MEP=90°,ME∥AB,
∴∠MPE+∠PME=90°,
∵四边形OABC是正方形,
∴∠POC=90°,OA=OC=AB=BC=4,∠BOA=45°,
∵PM⊥CP,
∴∠CPM=90°,
∴∠MPE+∠CPO=90°,
∴∠PME=∠CPO,
在△MPE和△PCO中,$\left\{\begin{array}{l}{∠MEP=∠POC=90°}&{\;}\\{∠PME=∠CPO}&{\;}\\{PM=CP}&{\;}\end{array}\right.$,
∴△MPE≌△PCO(AAS),
∴ME=PO=t,EP=OC=4,
∴OE=t+4,
∴点M的坐标为:(t+4,t);
(2)线段MN的长度不发生改变;理由如下:
连接AM,如图2所示: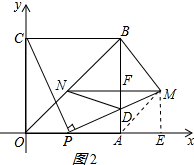
∵MN∥OA,ME∥AB,∠MEA=90°,
∴四边形AEMF是矩形,
又∵EP=OC=OA,
∴AE=PO=t=ME,
∴四边形AEMF是正方形,
∴∠MAE=45°=∠BOA,
∴AM∥OB,
∴四边形OAMN是平行四边形,
∴MN=OA=4;
(3)∵ME∥AB,
∴△PAD∽△PEM,
∴$\frac{AD}{ME}=\frac{AP}{EP}$,
即$\frac{AD}{t}=\frac{4-t}{4}$,
∴AD=-$\frac{1}{4}$t2+t,
∴BD=AB-AD=4-(-$\frac{1}{4}$t2+t)=$\frac{1}{4}$t2-t+4,
∵MN∥OA,AB⊥OA,
∴MN⊥AB,
∴四边形BNDM的面积S=$\frac{1}{2}$MN•BD=$\frac{1}{2}$×4($\frac{1}{4}$t2-t+4)=$\frac{1}{2}$(t-2)2+6,
∴S是t的二次函数,
∵$\frac{1}{2}$>0,
∴S有最小值,
当t=2时,S的值最小;
∴当t=2时,四边形BNDM的面积最小.
点评 本题是四边形综合题目,考查了正方形的性质与判定、全等三角形的判定与性质、平行四边形的判定与性质、相似三角形的判定与性质、四边形面积的计算以及二次函数的最值等知识;本题难度较大,综合性强,特别是(2)(3)中,需要证明四边形是正方形、平行四边形、三角形相似以及运用二次函数才能得出结果.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,将?ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
如图,将?ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | -20m | B. | 10m | C. | 20m | D. | -10m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为3.
如图,四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )
如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )| A. | 圆形铁片的半径是4cm | B. | 四边形AOBC为正方形 | ||
| C. | 弧AB的长度为4πcm | D. | 扇形OAB的面积是4πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
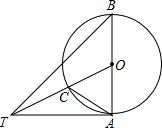 如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
如图,AB是⊙O的直径,∠ABT=45°,AT=AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.2918×105元 | B. | 6.2918×1014元 | C. | 6.2918×1013元 | D. | 6.2918×1012元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com