
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЪЧзјБъдЕуЃЌЕуBЃЈ0ЃЌ12ЃЉЃЌЕуAдкЕквЛЯѓЯоФкЃЌЁїAOBЮЊЕШбќШ§НЧаЮЃЌЁЯBAO=90ЁуЃЌAB=AOЃЌACЁЭOBЃЌЕуDДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛЕФЫйЖШбиyжсЯђжеЕуOдЫЖЏЃЌСЌНгDAЃЌЙ§ЕуAзїAEЁЭADЃЌЩфЯпAEНЛxжсгкЕуEЃЌСЌНгBEЃЌНЛЯпЖЮACгкЕуFЃЌНЛЯпЖЮOAгкЕуGЃЎ
ЃЈ1ЃЉЧыжБНгаДГіAЕФзјБъЃЛ
ЃЈ2ЃЉЕуDдЫЖЏЕФЪБМфЮЊtУыЪБЃЌгУКЌtЕФДњЪ§ЪНБэЪОЁїACDЕФУцЛ§SЃЌВЂаДГіtЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЫФБпаЮDAEOЕФУцЛ§ЕШгк6SЪБЃЌЧѓЁїAGFЕФУцЛ§ЃЎ
ЁЁ
ЁОД№АИЁПЃЈ1ЃЉAЃЈ6ЃЌ6ЃЉЃЛЃЈ2ЃЉЕБЕуDдкЯпЖЮBCЩЯЪБЃЈВЛАќРЈЕуCЃЉЃЌМДЃК0ЁмtЃМ3ЃЌS= 18Љ6tЃЌЕБЕуDдкЯпЖЮBCЩЯЪБЃЈВЛАќРЈЕуCЃЉЃЌМДЃК3ЃМtЁм6ЃЌЁрS= 6tЉ18ЃЛЃЈ3ЃЉЂйЕБЕуDдкЯпЖЮBCЩЯЪБЃЈВЛАќРЈЕуCЃЉЃЌМДЃК0ЁмtЃМ3ЃЌSЁїAFG=6ЃЛЂкЕБЕуDдкЯпЖЮOCЩЯЃЈВЛАќРЈЕуCЃЉЃЌМДЃК3ЃМtЁм6ЃЌSЁїAFG=![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШШЗЖЈГіOB=12ЃЌдйгУЕШбќжБНЧШ§НЧаЮЕФаджЪЕУAC=BC=OC=![]() OB=6ЃЌМДПЩЕУГіНсТлЃЛ
OB=6ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЕБЕуDдкЯпЖЮBCЩЯЪБЃЈВЛАќРЈЕуCЃЉЃЌМДЃК0ЁмtЃМ3ЃЌЕУГіCD=BC-BD=6-2tЃЌРћгУШ§НЧаЮУцЛ§ЙЋЪНМДПЩЃЛ
ЕБЕуDдкЯпЖЮBCЩЯЪБЃЈВЛАќРЈЕуCЃЉЃЌМДЃК3ЃМtЁм6ЃЌШчЭМ2ЃЌCD=BD-BC=2t-6ЃЌзюКѓРћгУШ§НЧаЮУцЛ§ЙЋЪНМДПЩЃЛ
ЃЈ3ЃЉЂйЕБЕуDдкЯпЖЮBCЩЯЪБЃЈВЛАќРЈЕуCЃЉЃЌМДЃК0ЁмtЃМ3ЃЌШчЭМ1ЃЌЯШХаЖЯГіSЁїACD=SЁїAMEЃЌНјЖјSЫФБпаЮDOEA=Sе§ЗНаЮACOM=AC2=36ЃЌМДПЩЧѓГіSЃЌНјЖјt=2ЃЌCD=EM=2ЃЌOE=4ЃЌдйЧѓГіAF=AC-CF=4=OEЃЌзюКѓХаЖЯГіЁїAFGЁеЁїOEGЃЌЧѓГіPG=QG=6МДПЩЕУГіНсТлЃЛ
ЂкЕБЕуDдкЯпЖЮOCЩЯЃЈВЛАќРЈЕуCЃЉЃЌМДЃК3ЃМtЁм6ЃЌШчЭМ2ЃЌЭЌЂйЕФЗНЗЈжЊЃЌS=6ЃЌt=4ЃЌCD=EM=2ЃЌOE=8ЃЌЭЌЂйЕФЗНЗЈЕУЃЌOF=4ЃЌМДAF=AC-OF=2ЃЌдйХаЖЯГіЁїAFGЁзЁїOEGЃЌЕУГіh'=4hЃЌМДПЩЕУГіh=![]() МДПЩЕУГіНсТлЃЎ
МДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЁпBЃЈ0ЃЌ12ЃЉЃЌ
ЁрOB=12ЃЌ
ЁпЁїAOBЮЊЕШбќШ§НЧаЮЃЌЁЯBAO=90ЁуЃЌAB=AOЃЌACЁЭOBЃЌ
ЁрAC=BC=OC=![]() OB=6ЃЌ
OB=6ЃЌ
ЁрAЃЈ6ЃЌ6ЃЉЃЛ
ЃЈ2ЃЉЕБЕуDдкЯпЖЮBCЩЯЪБЃЈВЛАќРЈЕуCЃЉЃЌМДЃК0ЁмtЃМ3ЃЌШчЭМ1ЃЌ
гЩдЫЖЏжЊЃЌBD=2tЃЌ
ЁрCD=BCЉBD=6Љ2tЃЌ
ЁрS=SЁїACD=![]() CDЁСAC=18Љ6tЃЌ
CDЁСAC=18Љ6tЃЌ
ЕБЕуDдкЯпЖЮBCЩЯЪБЃЈВЛАќРЈЕуCЃЉЃЌМДЃК3ЃМtЁм6ЃЌШчЭМ2ЃЌ
гЩдЫЖЏжЊЃЌBD=2tЃЌ
ЁрCD=BDЉBC=2tЉ6ЃЌ
ЁрS=SЁїACD=![]() CDЁСAC=6tЉ18ЃЛ
CDЁСAC=6tЉ18ЃЛ
ЃЈ3ЃЉЂйЕБЕуDдкЯпЖЮBCЩЯЪБЃЈВЛАќРЈЕуCЃЉЃЌМДЃК0ЁмtЃМ3ЃЌШчЭМ1ЃЌ
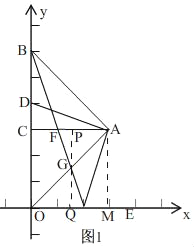
Й§ЕуAзїAMЁЭxжсгкMЃЌ
ЁрЫФБпаЮOCAMЪЧОиаЮЃЌ
ЁпAЃЈ6ЃЌ6ЃЉЃЌ
ЁрAC=AMЃЌ
ЁрОиаЮOCAMЪЧе§ЗНаЮЃЌ
ЁрOM=AC=6ЃЌЁЯCAM=90ЁуЃЌ
ЁпЁЯDAE=90ЁуЃЌ
ЁрЁЯCAD=ЁЯEAMЃЌ
дкЁїACDКЭЁїAMEжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїACDЁеЁїAMEЃЌ
ЁрSЁїACD=SЁїAMEЃЌ
ЁрSЫФБпаЮDOEA=SЁїACD+SЫФБпаЮCOEA=SЁїAMF+SЫФБпаЮCOEA=Sе§ЗНаЮACOM=AC2=36ЃЌ
ЁпЫФБпаЮDAEOЕФУцЛ§ЕШгк6SЃЌ
Ёр6S=36ЃЌ
ЁрS=6ЃЌ
гЩЃЈ2ЃЉжЊЃЌS=18Љ6tЃЌ
Ёр18Љ6t=6ЃЌ
Ёрt=2ЃЌ
ЁрCD=EM=6Љ2t=2ЃЌ
ЁпOM=6ЃЌ
ЁрOE=OMЉEM=4ЃЌ
ЁпACЁЮOMЃЌOC=BCЃЌ
ЁрCF=![]() OE=2ЃЌ
OE=2ЃЌ
ЁрAF=ACЉCF=4=OEЃЌ
Й§ЕуGзїGQЁЭOMгкQЃЌНЛACгкPЃЌ
ЁрPGЁЭACЃЌ
ЁрЫФБпаЮOCPQЪЧОиаЮЃЌ
ЁрPQ=OC=6ЃЌ
взжЊЃЌЁїAFGЁеЁїOEGЃЌ
ЁрPG=QG=6ЃЌ
ЁрSЁїAFG=![]() AFЁСPG=6ЃЛ
AFЁСPG=6ЃЛ
ЂкЕБЕуDдкЯпЖЮOCЩЯЃЈВЛАќРЈЕуCЃЉЃЌМДЃК3ЃМtЁм6ЃЌШчЭМ2ЃЌ

ЭЌЂйЕФЗНЗЈжЊЃЌS=6ЃЌ
ЁпS=6tЉ18ЃЌ
Ёр6tЉ18=6ЃЌ
Ёрt=4ЃЌ
ЁрCD=EM=2ЃЌ
ЁрOE=8ЃЌ
ЭЌЂйЕФЗНЗЈЕУЃЌOF=4ЃЌ
ЁрAF=ACЉOF=2ЃЌ
ЁпACЁЮOMЃЌ
ЁрЁїAFGЁзЁїOEGЃЌ
ЩшЁїAFGЕФБпAFЩЯЕФИпЮЊhЃЌЁїOEGЕФБпOEЩЯЕФИпЮЊh'ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёрh'=4hЃЌ
Ёпh+h'=6ЃЌ
Ёрh=![]() ЃЌ
ЃЌ
ЁрSЁїAFG=![]() AFЁСh=
AFЁСh=![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌMЪЧБпABЕФжаЕуЃЌСЌНгCMВЂбгГЄЕНЕуEЃЌЪЙЕУEM=![]() ABЃЌDЪЧБпACЩЯвЛЕуЃЌЧвAD=BCЃЌСЊНсDEЃЌЧѓЁЯCDEЕФЖШЪ§ЃЎ
ABЃЌDЪЧБпACЩЯвЛЕуЃЌЧвAD=BCЃЌСЊНсDEЃЌЧѓЁЯCDEЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAEЧаЁбOгкЕуEЃЌATНЛЁбOгкЕуMЃЌNЃЌЯпЖЮOEНЛATгкЕуCЃЌOBЁЭATгкЕуBЃЌвбжЊЁЯEAT=30ЁуЃЌAE=3 ![]() ЃЌMN=2
ЃЌMN=2 ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЁЯCOBЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓЁбOЕФАыОЖRЃЛ
ЃЈ3ЃЉЕуFдкЁбOЩЯЃЈ ![]() ЪЧСгЛЁЃЉЃЌЧвEF=5ЃЌАбЁїOBCОЙ§ЦНвЦЁЂа§зЊКЭЯрЫЦБфЛЛКѓЃЌЪЙЫќЕФСНИіЖЅЕуЗжБ№гыЕуEЃЌFжиКЯЃЎдкEFЕФЭЌвЛВрЃЌетбљЕФШ§НЧаЮЙВгаЖрЩйИіЃПФуФмдкЦфжаевГіСэвЛИіЖЅЕудкЁбOЩЯЕФШ§НЧаЮТ№ЃПЧыдкЭМжаЛГіетИіШ§НЧаЮЃЌВЂЧѓГіетИіШ§НЧаЮгыЁїOBCЕФжмГЄжЎБШЃЎ
ЪЧСгЛЁЃЉЃЌЧвEF=5ЃЌАбЁїOBCОЙ§ЦНвЦЁЂа§зЊКЭЯрЫЦБфЛЛКѓЃЌЪЙЫќЕФСНИіЖЅЕуЗжБ№гыЕуEЃЌFжиКЯЃЎдкEFЕФЭЌвЛВрЃЌетбљЕФШ§НЧаЮЙВгаЖрЩйИіЃПФуФмдкЦфжаевГіСэвЛИіЖЅЕудкЁбOЩЯЕФШ§НЧаЮТ№ЃПЧыдкЭМжаЛГіетИіШ§НЧаЮЃЌВЂЧѓГіетИіШ§НЧаЮгыЁїOBCЕФжмГЄжЎБШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧвЛИіе§ЗНЬхЕФБэУцеЙПЊЭМЃЌЧыЛиД№ЯТСаЮЪЬтЃК
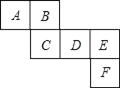
ЃЈ1ЃЉгыУцBЁЂCЯрЖдЕФУцЗжБ№ЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєAЃНa3+a2b+3ЃЌBЃНa2bЉ3ЃЌCЃНa3Љ1ЃЌDЃНЉЃЈa2bЉ6ЃЉЃЌЧвЯрЖдСНИіУцЫљБэЪОЕФДњЪ§ЪНЕФКЭЖМЯрЕШЃЌЧѓEЁЂFЗжБ№ДњБэЕФДњЪ§ЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЁЯABC=90ЁуЃЌЁїABCЪЧЕШбќШ§НЧаЮЃЌЕуDЮЊаББпACЕФжаЕуЃЌСЌНгDBЃЌЙ§ЕуAзїЁЯBACЕФЦНЗжЯпЃЌЗжБ№гыDBЃЌBCЯрНЛгкЕуEЃЌFЃЎ
ЃЈ1ЃЉЧѓжЄЃКBE=BFЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгCEЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЬѕМўЯТЃЌжБНгаДГіЭМжаЫљгаЕФЕШбќШ§НЧаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§ЕФЭМЯѓОЙ§AЃЈ2ЃЌ0ЃЉЁЂCЃЈ0ЃЌ12ЃЉСНЕуЃЌЧвЖдГЦжсЮЊжБЯпx=4ЃЎЩшЖЅЕуЮЊЕуPЃЌгыxжсЕФСэвЛНЛЕуЮЊЕуBЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНМАЖЅЕуPЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌдкжБЯп y=2xЩЯЪЧЗёДцдкЕуDЃЌЪЙЫФБпаЮOPBDЮЊЕШбќЬнаЮЃПШєДцдкЃЌЧѓГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуMЪЧЯпЖЮOPЩЯЕФвЛИіЖЏЕуЃЈOЁЂPСНЕуГ§ЭтЃЉЃЌвдУПУы ![]() ИіЕЅЮЛГЄЖШЕФЫйЖШгЩЕуPЯђЕуO дЫЖЏЃЌЙ§ЕуMзїжБЯпMNЁЮxжсЃЌНЛPBгкЕуNЃЎНЋЁїPMNбижБЯпMNЖделЃЌЕУЕНЁїP1MNЃЎдкЖЏЕуMЕФдЫЖЏЙ§ГЬжаЃЌЩшЁїP1MNгыЬнаЮOMNBЕФжиЕўВПЗжЕФУцЛ§ЮЊSЃЌдЫЖЏЪБМфЮЊtУыЃЎЧѓSЙигкtЕФКЏЪ§ЙиЯЕЪНЃЎ
ИіЕЅЮЛГЄЖШЕФЫйЖШгЩЕуPЯђЕуO дЫЖЏЃЌЙ§ЕуMзїжБЯпMNЁЮxжсЃЌНЛPBгкЕуNЃЎНЋЁїPMNбижБЯпMNЖделЃЌЕУЕНЁїP1MNЃЎдкЖЏЕуMЕФдЫЖЏЙ§ГЬжаЃЌЩшЁїP1MNгыЬнаЮOMNBЕФжиЕўВПЗжЕФУцЛ§ЮЊSЃЌдЫЖЏЪБМфЮЊtУыЃЎЧѓSЙигкtЕФКЏЪ§ЙиЯЕЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABDКЭЁїBCDЖМЪЧЕШБпШ§НЧаЮжНЦЌЃЌAB=2ЃЌНЋЁїABDжНЦЌЗелЃЌЪЙЕуAТфдкCDЕФжаЕуEДІЃЌелКлЮЊFGЃЌЕуFЁЂGЗжБ№дкБпABЁЂADЩЯЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїFBEЪЧжБНЧШ§НЧаЮЃЛ
ЃЈ2ЃЉЧѓBFЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=4ЃЌAC=6ЃЌЁЯABCКЭЁЯACBЕФЦНЗжЯпНЛгкЕуEЃЌЙ§ЕуEзїMNЁЮBCЗжБ№НЛABЁЂACгкMЁЂNЃЌдђЁїAMNЕФжмГЄЮЊЃЈЁЁЁЁЃЉ

A. 10 B. 6 C. 4 D. ВЛШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌADКЭAEЗжБ№ЪЧЁїABCЕФBCБпЩЯЕФИпКЭжаЯпЃЌЕуDЪЧДЙзуЃЌЕуEЪЧBCЕФжаЕуЃЌЙцЖЈЃКІЫA= ![]() ЃЎЬиБ№ЕиЃЌЕБЕуDЁЂEжиКЯЪБЃЌЙцЖЈЃКІЫA=0ЃЎСэЭтЃЌЖдІЫBЁЂІЫCзїРрЫЦЕФЙцЖЈЃЎ
ЃЎЬиБ№ЕиЃЌЕБЕуDЁЂEжиКЯЪБЃЌЙцЖЈЃКІЫA=0ЃЎСэЭтЃЌЖдІЫBЁЂІЫCзїРрЫЦЕФЙцЖЈЃЎ
ЃЈ1ЃЉШчЭМ2ЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯA=30ЁуЃЌЧѓІЫAЁЂІЫCЃЛ
ЃЈ2ЃЉдкУПИіаЁе§ЗНаЮБпГЄОљЮЊ1ЕФ4ЁС4ЕФЗНИёжНЩЯЃЌЛвЛИіЁїABCЃЌЪЙЦфЖЅЕудкИёЕуЃЈИёЕуМДУПИіаЁе§ЗНаЮЕФЖЅЕуЃЉЩЯЃЌЧвІЫA=2ЃЌУцЛ§вВЮЊ2ЃЛ
ЃЈ3ЃЉХаЖЯЯТСаШ§ИіУќЬтЕФецМйЃЈецУќЬтДђЁАЁЬЁБЃЌМйУќЬтДђЁАЁСЁБЃЉЃК
ЂйШєЁїABCжаІЫAЃМ1ЃЌдђЁїABCЮЊШёНЧШ§НЧаЮЃЛ
ЂкШєЁїABCжаІЫA=1ЃЌдђЁїABCЮЊжБНЧШ§НЧаЮЃЛ
ЂлШєЁїABCжаІЫAЃО1ЃЌдђЁїABCЮЊЖлНЧШ§НЧаЮЃЎ ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com