
分析 (1)先算幂的乘方,再根据同底数幂的乘除法法则计算即可求解;
(2)根据同底数幂的乘除法法则计算即可求解;
(3)先算积的乘方,再根据同底数幂的乘除法法则计算即可求解;
(4)先算积的乘方,再根据同底数幂的乘除法法则计算,最后合并同类项即可求解;
(5)先算乘方,零指数幂和负整数指数幂,再相加即可求解;
(6)逆用积的乘方计算即可求解.
解答 解:(1)(-a3)4•(-a2)5;
=a12•(-a10)
=-a22;
(2)(p-q)4÷(p-q)3•(p-q)2;
=(p-q)4-3+2
=(p-q)3;
(3)(a2bc)4÷(ab2c)3•(abc)2(abc≠0)
=a8b4c4÷a3b6c3•a2b2c2
=a7c3;
(4)(-2x)5-(-x)3•(-2x)2
=-32x5+4x5
=-28x5;
(5)(-1)2015+2-1-($\frac{3}{2}$)-2+(π-3.14)0
=-1+$\frac{1}{2}$-$\frac{4}{9}$+1
=$\frac{1}{18}$;
(6)(-0.125)12×(-1$\frac{2}{3}$)7×(-8)13×(-$\frac{3}{5}$)8
=(0.125×8)12×(1$\frac{2}{3}$×$\frac{3}{5}$)7×(-8)×(-$\frac{3}{5}$)
=1×1×(-8)×(-$\frac{3}{5}$)
=$\frac{24}{5}$.
点评 考查了整式的混合运算,注意:(1)有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.(2)“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.同时考查了实数的运算.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:选择题
| 甲的成绩 | 6 | 7 | 8 | 8 | 9 | 9 |
| 乙的成绩 | 5 | 9 | 6 | ? | 9 | 10 |
| A. | 6环 | B. | 7环 | C. | 8环 | D. | 9环 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
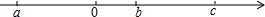 实数a,b,c在数轴上的位置如图所示.
实数a,b,c在数轴上的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
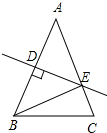 在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )
在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
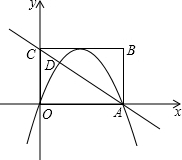 如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=8,OC=6,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.
如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=8,OC=6,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com