
(10分)如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.

(1)问几秒后△PBQ的面积等于8cm2?
(2)是否存在这样的时刻,使 =8cm2,试说明理由.
=8cm2,试说明理由.
科目:初中数学 来源:2016届江苏省盐城市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.

(1)求船P到海岸线MN的距离;
(2)若船A、船B分别以20海里/时、15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源:2016届江苏省盐城市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( )

A、2 B、2 C、4 D、4
C、4 D、4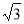
查看答案和解析>>
科目:初中数学 来源:2016届江苏省九年级上学期第一次月考数学试卷(解析版) 题型:计算题
(本题满分12分)
知识迁移
当 且
且 时,因为
时,因为 ≥
≥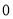 ,所以
,所以 ≥
≥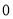 ,从而
,从而 ≥
≥ (当
(当 时取等号).
时取等号).
记函数 ,由上述结论可知:当
,由上述结论可知:当 时,该函数有最小值为
时,该函数有最小值为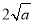 .
.
直接应用
已知函数 与函数
与函数 ,则当
,则当 时,
时, 取得最小值为 .
取得最小值为 .
变形应用
已知函数 与函数
与函数 ,求
,求 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的 的值.
的值.
实际应用
已知某汽车的 一次运输成本包含以下三个部分:一是固定费用,共
一次运输成本包含以下三个部分:一是固定费用,共 元;二是燃油费,每千米为
元;二是燃油费,每千米为 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为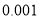 .设该汽车一次运输的路程为
.设该汽车一次运输的路程为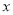 千米,求当
千米,求当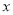 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
查看答案和解析>>
科目:初中数学 来源:2016届江苏省九年级上学期第一次月考数学试卷(解析版) 题型:填空题
如图,AB是⊙O的直径,∠ACB=90°.弦BC=2cm,点 F是弦BC的中点,∠ABC=60°.若动点E从A点出发沿着A→B方向运动,连接EF、CE,则EF+CE最小值是 .

查看答案和解析>>
科目:初中数学 来源:2016届湖北省武汉市东西湖区九年级上学期期中考试数学试卷(解析版) 题型:解答题
一个二次函数的图像经过(0,-2),(-1,-1),(1,1)三点,求这个二次函数的解析式
查看答案和解析>>
科目:初中数学 来源:2015-2016学年内蒙古乌海市八年级上学期期中考试数学试卷(解析版) 题型:选择题
若三角形中最大内角是60°,则这个三角形是( )
A.不等边三角 B.等腰三角形 C.等边三角形 D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com