
【题目】如图,四边形OP1A1B1、A1P2A2B2、A2P3A3B3、……、An-1PnAnBn都是正方形,对角线OA1、A1A2、A2A3、……、An-1An都在y轴上(n≥2),点P1(x1,y1),点P2(x2,y2),……,点Pn(xn,yn)在反比例函数y=![]() (x>0)的图象上,已知B1 (-1,1)。
(x>0)的图象上,已知B1 (-1,1)。
(1)反比例函数解析式为________;
(2)求点P1和点P2的坐标;
(3)点Pn的坐标为(____________)(用含n的式子表示),△PnBnO的面积为__________。(直接填答案)

【答案】 y=![]() Pn(
Pn(![]() -
-![]() ,
,![]() +
+![]() ) 1
) 1
【解析】(1)由四边形OP1A1B1为正方形且OA1是对角线知B1与P1关于y轴对称,得出点P1(1,1),据此可得答案;
(2)连接P2B2、P3B3,分别交y轴于点E、F,由点P1坐标及正方形的性质知OA1=2,据此可设P2的坐标为(a,a+2),代入解析式求得a的值即可,同理可得点P3的坐标;
(3)由![]() =2
=2![]() =2×
=2×![]() =1,
=1,![]() =2
=2![]() =2×
=2×![]() =1可知△PnBnO的面积为1,根据P1(1,1)、P2(
=1可知△PnBnO的面积为1,根据P1(1,1)、P2(![]() ﹣1,
﹣1,![]() +1)、P3(
+1)、P3(![]() ﹣
﹣![]() +
+![]() )知点Pn的坐标为(
)知点Pn的坐标为(![]() ﹣
﹣![]() +
+![]() ).
).
(1)在正方形OP1A1B1中,OA1是对角线,则B1与P1关于y轴对称.
∵B1(﹣1,1),∴P1(1,1).
则k=1×1=1,即反比例函数解析式为y=![]() ;
;
(2)连接P2B2、P3B3,分别交y轴于点E、F, 又点P1的坐标为(1,1),∴OA1=2,设点P2的坐标为(a,a+2),代入y=![]() 得:a=
得:a=![]() ﹣1,故点P2的坐标为(
﹣1,故点P2的坐标为(![]() ﹣1,
﹣1,![]() +1),则A1E=A2E=
+1),则A1E=A2E=![]() ﹣1,OA2=OA1+A1A2=2
﹣1,OA2=OA1+A1A2=2![]() ,设点P3的坐标为(b,b+2
,设点P3的坐标为(b,b+2![]() ),代入y=
),代入y=![]() (x>0)可得:b=
(x>0)可得:b=![]() ﹣
﹣![]() ,故点P3的坐标为(
,故点P3的坐标为(![]() ﹣
﹣![]() +
+![]() ).
).

(3)∵![]() =2
=2![]() =2×
=2×![]() =1,
=1,![]() =2
=2![]() =2×
=2×![]() =1,…
=1,…
∴△PnBnO的面积为1,由P1(1,1)、P2(![]() ﹣1,
﹣1,![]() +1)、P3(
+1)、P3(![]() ﹣
﹣![]() +
+![]() ),知点Pn的坐标为(
),知点Pn的坐标为(![]() ﹣
﹣![]() +
+![]() ).
).
故答案为:(![]() ﹣
﹣![]() +
+![]() ),1.
),1.


科目:初中数学 来源: 题型:
【题目】在元旦期间,某商场投入13800元资金购进甲、乙两种商品共500件,两种商品的成本价和销售价如下表所示:
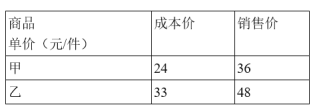
(1)该商场购进两种商品各多少件?
(2)这批商品全部销售完后,该商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
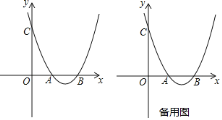
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
![]() 填空:
填空:![]() ________;
________;
![]() 点
点![]() 在抛物线上,且
在抛物线上,且![]() ,求
,求![]() 面积的最大值;
面积的最大值;
![]() 设
设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒一个单位速度运动到
以每秒一个单位速度运动到![]() 点,再沿线段
点,再沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止,当点
后停止,当点![]() 的坐标是多少时,点
的坐标是多少时,点![]() 在整个运动中用时最少?
在整个运动中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
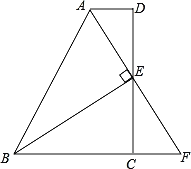
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形A'B'C'D'在矩形ABCD的内部,AB∥A'B',AD∥A'D',且AD=12,AB=6,设AB与A'B'、BC与B'C'、CD与C'D'、DA与D'A'之间的距离分别为a,b,c,d,
(1)a=b=c=d=2,矩形A'B'C'D'∽矩形ABCD吗,为什么?
(2)若矩形A'B'C'D'∽矩形ABCD,a,b,c,d应满足什么等量关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角三角形ABC中,∠ACB=90°,BC=m,将边AB绕点B顺时针旋转90°得到线段BD,过点D作DE⊥CB交CB的延长线于点E,连接CD.
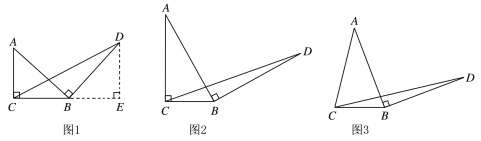
(1)直接写出△BCD的面积为 (用含m的式子表示).
(2)如图2,在一般的Rt△ABC中,∠ACB=90°,BC=m,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,用含m的式子表示△BCD的面积,并说明理由.
(3)如图3,在等腰△ABC中,AB=AC,BC=8,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,则△BCD的面积为 ;若BC=m,则△BCD的面积为 (用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角坐标平面内的两点A(3,2),点B (6,0)过点B作Y轴的平行线交直线OA于点C
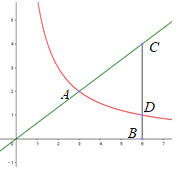
(1)求直线OA所对应的函数解析式
(2)若某一个反比例函数的图像经过点A,且交BC于点D,联结AD,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.

(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1) 先证明△DOP≌△EOH,再利用等量代换得到PE=DH.
(2) 设DP=x, Rt△BCH中,先用 x表示三角形三边,利用勾股定理列式解方程.
试题解析:
(1)解:证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH,
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH.
(2)解:设DP=x,则EH=x,BH=10﹣x,
CH=CD﹣DH=CD﹣PE=10﹣(8﹣x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10﹣x)2,
∴x=![]() ,
,
∴DP=![]() .
.
【题型】解答题
【结束】
25
【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com