
【题目】在x轴上有点P(a,0)(其中a>2),过点P作x斜的蓬线,分别交函数 ![]() 和
和 ![]() 的图象于点C、D。
的图象于点C、D。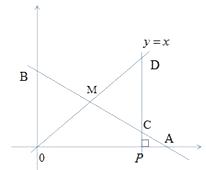
(1)求点A的坐标
(2)若OB=CD,求a的值
(3)在(2)条件下若以0D线段为边,作正方形0DEF,求直线EF的表达式。
【答案】
(1)解:∵点M在直线y=x的图象上,且点M的横坐标为2,
∴点M的坐标为(2,2),
把M(2,2)代入y=-![]() x+b得-1+b=2,解得b=3,
x+b得-1+b=2,解得b=3,
∴一次函数的解析式为y=-x+3,
把y=0代入y=-![]() x+3得-
x+3得-![]() x+3=0,解得x=6,
x+3=0,解得x=6,
∴A点坐标为(6,0);
(2)把x=0代入y=-1
2x+3得y=3,
∴B点坐标为(0,3),
∵CD=OB,
∴CD=3,
∵PC⊥x轴,
∴C点坐标为(a,-![]() a+3),D点坐标为(a,a)
a+3),D点坐标为(a,a)
∴a-(-![]() a+3)=3,
a+3)=3,
∴a=4.
(3)由(2)知,OD=4![]() ,∵四边形ODEF为正方形,∴EF
,∵四边形ODEF为正方形,∴EF![]() OD,且EF=OD,直线EF相当于直线OD向下平移8个单位得到的,∴直线EF 的表达式为y=x-8.
OD,且EF=OD,直线EF相当于直线OD向下平移8个单位得到的,∴直线EF 的表达式为y=x-8.
【解析】(1)先利用直线y=x上的点的坐标特征得到点M的坐标为(2,2),再把M(2,2)代入y=-1
2x+b可计算出b=3,得到一次函数的解析式为y=-![]() x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6,0);
x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6,0);
(2)先确定B点坐标为(0,3),则OB=CD=3,再表示出C点坐标为(a,-![]() a+3),D点坐标为(a,a),所以a-(-
a+3),D点坐标为(a,a),所以a-(-![]() a+3)=3,然后解方程即可
a+3)=3,然后解方程即可
(3)利用正方形的性质,OD 平行且等于EF,可利用平移关系求出EF的表达式.


科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( ) 
A.(a+b)2=a2+2ab+b2
B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a+2b)(a﹣b)=a2+ab﹣2b2
查看答案和解析>>
科目:初中数学 来源: 题型:
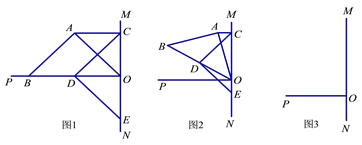
【题目】已知O为直线MN上一点,OP⊥MN,在等腰Rt△ABO中, ![]() ,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.
,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.
(1) 如图1,若点B在OP上,则①AC OE(填“<”,“=”或“>”);②线段CA、CO、CD满足的等量关系式是 ;
(2) 将图1中的等腰Rt△ABO绕O点顺时针旋转(![]() ),如图2,那么(1)中的结论②是否成立?请说明理由;
),如图2,那么(1)中的结论②是否成立?请说明理由;
(3) 将图1中的等腰Rt△ABO绕O点顺时针旋转(),请你在图3中画出图形,并直接写出线段CA、CO、CD满足的等量关系式 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一蚂蚁从原点![]() 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
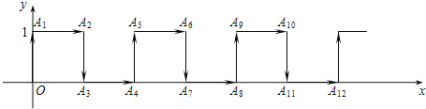
(1)填写下列各点的坐标:![]() (____,____),
(____,____),![]() (____,____),
(____,____),![]() (____,____);
(____,____);
(2)写出点![]() 的坐标(n是正整数);
的坐标(n是正整数);
(3)指出蚂蚁从点![]() 到
到![]() 的移动方向.
的移动方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
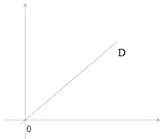
【题目】如图所示,左右两幅图案关于y轴对称,右边图案中的左、右两朵花花心的坐标分别是(2,5)和(3,4).
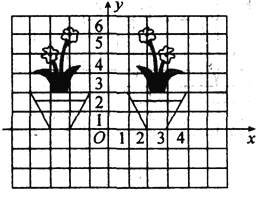
(1)试确定左边图案中的左、右两朵花花心的坐标.
(2)如果将右边图案沿x轴向右平移2个单位长度,那么它的左、右两朵花的花心坐标将发生什么变化?
(3)如果将右边图案中的所有点的横坐标保持不变,纵坐标都加1,那么图案将发生什么变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市前年PM2.5的年均浓度为50微克/立方米,去年比前年下降了10%,如果今年PM2.5的年均浓度比去年也下降10%,那么今年PM2.5的年均浓度将是微克/立方米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com