Question

13．问题背景：如图1，要在街道MN旁修建一个奶站，向A，B两居民区供奶，奶站应建在什么地方，才能使A，B到奶站的距离之和最小？在解决这一问题时，我们以MN为对称轴，作A的对称点A₁，连接A₁B，此时P点到A，B的距离和最短，这其中的道理是两点之间线段最短．
探究发现：
如图2，为已知点P是∠AOB内任意一点，点P₁，P关于OA对称，点P₂，P关于OB对称．连接P₁P₂，分别交OA，OB于C，D．连接PC，PD．若P₁P₂=14cm，则△PCD的周长14cm．
拓展迁移：
电信部门要修建A，B两座电视信号发射塔，如图3，按照设计要求，发射塔要分别建在两条高速公路m，n 上，并且与城镇C三点之间的距离和最小，发射塔应建在什么位置？（不写作法，保留作图痕迹）

Answer 1

分析 问题背景：两点之间线段最短，
探究发现：根据对称性PC=P₁C，PD=P₂D，最后转化即可；
拓展迁移：过点C分别作直线m，n的垂线，作出对称点，连接C'C“，和直线m，n的交点就是发射塔．

解答 解：问题背景：两点之间线段最短，
故答案为：两点之间线段最短；
探究发现：
∵点P₁，P关于OA对称，
∴PC=P₁C，
∵点P₂，P关于OB对称，
∴PD=P₂D，
∴△PCD的周长=PC+PD+CD=P₁C+P₂D+CD=P₁P₂=14cm，
故答案为：14cm；
拓展迁移：
如图3，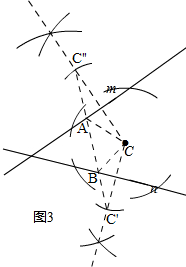

∴A，B两座电视信号发射塔应建在如图3所示的位置．

点评 此题是三角形综合题，主要考查了垂直平分线的性质，对称性，解本题的关键是掌握作点关于直线的对称点．