
【题目】如图,△ABC中, D、E是AB上的两点,△CDE是等边三角形.
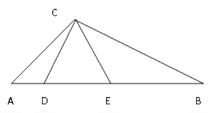
求证:(1)△ABC∽△ACD;
(2)△ACD∽△CBE;
(3)![]() .
.
【答案】(1)详见解析;(2)详见解析;(3)见解析.
【解析】
(1)找到公共角∠A,再genju 等量代换得到∠ADC=120°=∠ACB,即可证明相似.
(2)由(1)得到∠ACD=∠B,再可得∠ADC=120°=∠CEB,即可证明相似.
(3)由(2)得△ACD∽△CEB,则![]() ,由CD=CE=DE,等量代换即可证明.
,由CD=CE=DE,等量代换即可证明.
(1)∵△CDE是等边三角形
∴∠CDE=60°
∴∠ADC=120°=∠ACB
又∵∠A=∠A
∴△ABC∽△ACD
(2)∵△CDE是等边三角形
∴∠CDE=60°=∠CED CD=CE=DE
∴ ∠ADC=120°=∠CEB
又∵△ABC∽△ACD
∴∠ACD=∠B
∴△ACD∽△CEB
(3) ∵△ACD∽△CEB
∴![]()
又∵ CD=CE=DE
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是( )
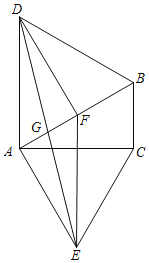
A.①③B.②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,若AC=6,则DE的长为( )
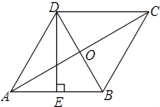
A. 3 B. 3![]() C. 2
C. 2![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
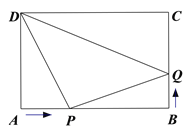
【题目】如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ的面积是24cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自1993年起,联合国将每年的3月22日定为“世界水日”,宗旨是唤起公众的节水意识,加强水资源保护.某校在开展“节约每一滴水”的活动中,从初三年级随机选出20名学生统计出各自家庭一个月的节约用水量,有关数据整理如下表.
节约用水量(单位:吨) | 1 | 1.2 | 1.4 | 2 | 2.5 |
家庭数 | 4 | 6 | 5 | 3 | 2 |
这组数据的中位数和众数分别是( )
A. 1.2,1.2; B. 1.4,1.2; C. 1.3,1.4; D. 1.3,1.2.
查看答案和解析>>
科目:初中数学 来源: 题型:
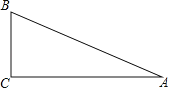
【题目】如图,![]() 是直角三角形,
是直角三角形,![]() .
.
(1)动手操作:利用尺规作![]() 的平分线,交
的平分线,交![]() 于点
于点![]() ,再以
,再以![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() (保留作图痕迹,不写作法);
(保留作图痕迹,不写作法);
(2)综合运用:请根据所作的图,
①判断![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.一组数据﹣2,﹣1,0,1,1,2的中位数是0
B.质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式
C.购买一张福利彩票中奖是一个确定事件
D.分别写有三个数字﹣1,﹣2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com