
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 12元 | 10元 | 8元 |
分析 (1)首先设一班x人,二班y人,由题意得等量关系:①两班共102人;②一班的花费+二班的花费=1118元,根据等量关系列出方程组,再解即可;
(2)两班联合购票花费为8×102,然后再用1118元减去8×102即可.
解答 解:(1)设一班x人,二班y人,由题意得:
$\left\{\begin{array}{l}{x+y=102}\\{12x+10y=1118}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=49}\\{y=53}\end{array}\right.$.
答:一班49人,二班53人;
(2)1118-8×102=302(元),
答:两班联合起来购票能节省302元.
点评 此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{x+1}$ | B. | $\sqrt{x-1}$ | C. | $\sqrt{x}$+1 | D. | $\sqrt{x}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
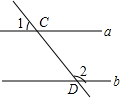 如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )
如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )| A. | 135° | B. | 145° | C. | 155° | D. | 165° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
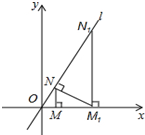 如图,已知直线l:y=$\sqrt{3}x$(直线l与x轴的夹角是60°),过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点Mn的坐标为(22n+1,0).
如图,已知直线l:y=$\sqrt{3}x$(直线l与x轴的夹角是60°),过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点Mn的坐标为(22n+1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
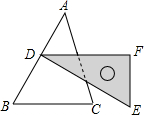 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,若∠B为锐角,BC∥DF,则∠B的大小为60°.
如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,若∠B为锐角,BC∥DF,则∠B的大小为60°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.3}$ | B. | $\sqrt{10}$ | C. | $\sqrt{20}$ | D. | $\sqrt{24}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com