
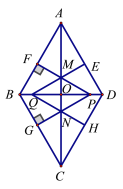
【题目】如图:菱形ABCD的对角线AC,BD相交于点O,AC=![]() ,BD=
,BD=![]() ,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,PG⊥BC于点G,四边形QEDH与四边形PFBG关于点O中心对称,设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,
,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,PG⊥BC于点G,四边形QEDH与四边形PFBG关于点O中心对称,设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,![]() ,若S1=S2,则
,若S1=S2,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D. 不存在
D. 不存在
【答案】A
【解析】
根据对称性确定E、F、G、H都在菱形的边上,由于点P在BO上与点P在OD上求S1和S2的方法不同,因此需分情况讨论,由S1=S2和S1+S2=8![]() 可以求出S1=S2=4
可以求出S1=S2=4![]() .然后在两种情况下分别建立关于x的方程,解方程,结合不同情况下x的范围确定x的值.
.然后在两种情况下分别建立关于x的方程,解方程,结合不同情况下x的范围确定x的值.
①当点P在BO上,0<x≤2时,如图1所示.
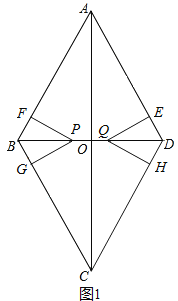
∵四边形ABCD是菱形,AC=4![]() ,BD=4,
,BD=4,
∴AC⊥BD,BO=![]() BD=2,AO=
BD=2,AO=![]() AC=2
AC=2![]() ,
,
且S菱形ABCD=![]() BDAC=8
BDAC=8![]() .
.
∴tan∠ABO=![]() =
=![]() .
.
∴∠ABO=60°.
在Rt△BFP中,
∵∠BFP=90°,∠FBP=60°,BP=x,
∴sin∠FBP=![]() .
.
∴FP=![]() x.
x.
∴BF=![]() .
.
∵四边形PFBG关于BD对称,
四边形QEDH与四边形PEBG关于AC对称,
∴S△BFP=S△BGP=S△DEQ=S△DHQ.
∴S1=4S△BFP
=4×![]() ×
×![]() x
x![]()
=![]() x2.
x2.
∴S2=8![]() -
-![]() x2.
x2.
②当点P在OD上,2<x≤4时,如图2所示.

∵AB=4,BF=![]() ,
,
∴AF=AB-BF=4![]() .
.
在Rt△AFM中,
∵∠AFM=90°,∠FAM=30°,AF=4-![]() .
.
∴tan∠FAM=![]() .
.
∴FM=![]() (4-
(4-![]() ).
).
∴S△AFM=![]() AFFM
AFFM
=![]() (4-
(4-![]() )
)![]() (4-
(4-![]() )
)
=![]() (4-
(4-![]() )2.
)2.
∵四边形PFBG关于BD对称,
四边形QEDH与四边形FPBG关于AC对称,
∴S△AFM=S△AEM=S△CHN=S△CGN.
∴S2=4S△AFM
=4×![]() (4-
(4-![]() )2
)2
=![]() (x-8)2.
(x-8)2.
∴S1=8![]() -S2=8
-S2=8![]() -
-![]() (x-8)2.
(x-8)2.
综上所述:
当0<x≤2时,S1=![]() x
x![]() -
-![]() x2;
x2;
当2<x≤4时,S1=8![]() -
-![]() (x-8)2,S2=
(x-8)2,S2=![]() (x-8)2.
(x-8)2.
当点P在BO上时,0<x≤2.
∵S1=S2,S1+S2=8![]() ,
,
∴S1=4![]() .
.
∴S1=![]() x2=4
x2=4![]() .
.
解得:x1=2![]() ,x2=-2
,x2=-2![]() .
.
∵2![]() >2,-2
>2,-2![]() <0,
<0,
∴当点P在BO上时,S1=S2的情况不存在.
当点P在OD上时,2<x≤4.
∵S1=S2,S1+S2=8![]() ,
,
∴S2=4![]() .
.
∴S2=![]() (x-8)2=4
(x-8)2=4![]() .
.
解得:x1=8+2![]() ,x2=8-2
,x2=8-2![]() .
.
∵8+2![]() >4,2<8-2
>4,2<8-2![]() <4,
<4,
∴x=8-2![]() .
.
综上所述:若S1=S2,则x的值为8-2![]() .
.
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
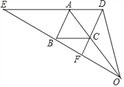
【题目】如图,已知DE∥BC,AO,DF交于点C.∠EAB=∠BCF.
(1)求证:AB∥DF;
(2)求证:OB2=OEOF;
(3)连接OD,若∠OBC=∠ODC,求证:四边形ABCD为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
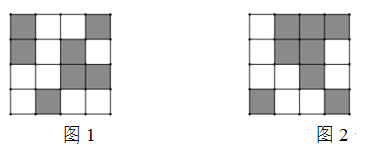
【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式a×23-b×22-c×21+d计算出每一行的数据.第一行表示年级,第二行表示班级,如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的编号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
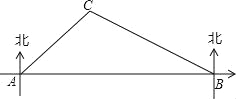
【题目】如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=400m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E、F分别是□ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=2cm2,S△BQC=4cm2,则阴影部分的面积为( )
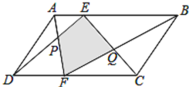
A. 6 cm2B. 8 cm2C. 10 cm2D. 12 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有3个黑球和若干白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,…不断重复上述过程.小明共摸100次,其中20次摸到黑球.根据上述数据,小明估计口袋中白球大约有( )
A. 10个 B. 12 个 C. 15 个 D. 18个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级所有女生的身高统计数据如下表,请回答下列问题:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) 这个学校八年级共有多少女生?
(2) 身高在 ![]() 到
到 ![]() 的女生有多少人?
的女生有多少人?
(3) 一女生的身高恰好为 ![]() ,哪一组包含这个身高?这一组出现的频数、频率各是多少?
,哪一组包含这个身高?这一组出现的频数、频率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a,b,c,其中a,b是直角边,正方形的边长分别是a、b.
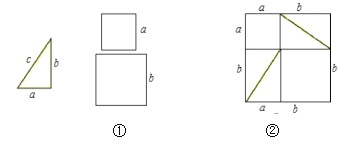
(1)将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形面积:
方法一:______________________________;
方法二:______________________________;
(2)观察图②,试写出![]() ,
,![]() ,
,![]() ,
,![]() 这四个代数式之间的等量关系;
这四个代数式之间的等量关系;
(3)利用(2)的结论计算![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com