练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某商品的进价为每件40元，当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：

    （1）若设每件降价x元、每星期售出商品的利润为y元，请写y与x函数关系式，并求出自变量x的取值范围

    （2）当降价多少元时，每星期的利润最大？最大利润是多少元?

    【答案】（1）y=-20x2+100x+6000， 0≤x＜20；（2）2.5，6125.

    【解析】

    （1）用每件商品的利润乘每星期所售出的件数就可以得出每星期售出商品的利润；x为正整数，即可求出x的取值范围；
    （2）由（1）的函数解析式直接配方求出最值即可；

    解：（1）若设每件降价x元、每星期售出商品的利润为y元，
    则y=（300+20x）（60-40-x）
    =-20x2+100x+6000；
    且40＜60-x≤60，即0≤x＜20；
    （2）由（1）得
    y=-20x2+100x+6000
    =-20（x-）2+6125；
    当x=时有最大值6125.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A，C分别在x轴，y轴上，四边形ABCO为矩形，AB=16，AC=20,点D与点A关于y轴对称，点E、F分别是线段AD、AC上的动点（点E不与点A、D重合），且∠CEF=∠ACB.

    （1）直接写出BC的长是　 　，点D的坐标是　 　；

    （2）证明：△AEF与△DCE相似；

    （3）当△EFC为等腰三角形时，求点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（5，0）两点．

    （1）求抛物线y＝﹣x2+bx+c的解析式．

    （2）在第二象限内取一点C，作CD⊥x轴于点D，连接AC，且AD＝1，CD＝5，将Rt△ACD沿x轴向右平移m个单位．

    ①当点C第一次落在抛物线上时，求m的值．

    ②当△ACD与抛物线y＝﹣x2+bx+c的图象有交点时，求m的取值范围（直接答案即可）

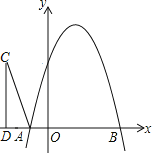
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一个三角形一条边的平方等于另两条边的乘积，我们把这个三角形叫做比例三角形．

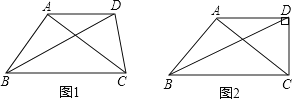
    （1）已知△ABC是比例三角形，AB＝3，BC＝4，请直接写出所有满足条件的AC的长；

    （2）如图1，在四边形ABCD中，AD∥BC，对角线BD平分∠ABC，∠BAC＝∠ADC．求证：△ABC是比例三角形；

    （3）如图2，在（2）的条件下，当∠ADC＝90°时，求出的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，过点B作BE⊥CD，垂足为E，连接AE．F为AE上一点，且∠BFE＝∠C．

    （1）试说明：△ABF∽△EAD；

    （2）若AB＝8，BE＝6，AD＝9，求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一种落地晾衣架如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度. 图2是支撑杆的平面示意图，AB和CD分别是两根不同长度的支撑杆，夹角∠BOD=. 若AO=85cm，BO=DO=65cm. 问: 当，较长支撑杆的端点离地面的高度约为_____.(参考数据:，.)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，C地在A地的正东方向，因有大山阻隔，由A地到C地需绕行B地，已知B地位于A地北偏东67°方向，距离A地520km，C地位于B地南偏东30°方向，若打通穿山隧道，建成两地直达高铁，求A地到C地之间高铁线路的长．（结果保留整数）

    （参考数据：sin67°≈，cos67°≈，tan67°≈，≈1.73）

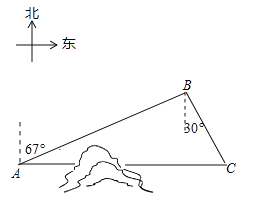
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某玩具商店以成本为每件60元购进一批新型玩具，以每件100元的价格销售则每天可卖出20件，为了扩大销售，增加盈利，尽快减少库存，商店决定采取适当的降价措施，经调查发现：若每件玩具每降价5元，则每天可多卖10件.

    (1)若商店平均每天盈利1200元，每件玩具的售价应定为多少元？

    (2)若商店为增加效益最大化，每件玩具的售价定为多少元时，商店平均每天盈利最多？最多盈利多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）先化简，再求值：其中，a是方程x2+3x+1＝0的根．

    （2）已知抛物线y＝ax2+bx+c的对称轴为x＝2，且经过点（1，4）和（5，0），试求该抛物线的表达式．

    查看答案和解析>>

    同步练习册答案