
【题目】如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,AC=20,点D与点A关于y轴对称,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
(1)直接写出BC的长是 ,点D的坐标是 ;
(2)证明:△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标.

【答案】(1) A(-12,0),D(12,0);(2)证明见解析;(3)点E的坐标为(8,0)或(![]() ,0).
,0).
【解析】试题分析:(1)利用矩形的性质,在![]() 中,利用三角函数求出
中,利用三角函数求出![]() 的长度,从而得到
的长度,从而得到![]() 点坐标;由点
点坐标;由点![]() 与点
与点![]() 关于
关于![]() 轴对称,进而得到
轴对称,进而得到![]() 点的坐标;
点的坐标;
(2)欲证△AEF与△DCE相似,只需要证明两个对应角相等即可.如图①,在△AEF与△DCE中,易知![]() 从而问题解决;
从而问题解决;
(3)当![]() 为等腰三角形时,有三种情况,需要分类讨论:
为等腰三角形时,有三种情况,需要分类讨论:
①当![]() 时,此时△AEF与△DCE相似比为1,则有
时,此时△AEF与△DCE相似比为1,则有![]()
②当![]() 时,此时△AEF与△DCE相似比为
时,此时△AEF与△DCE相似比为![]() ,则有
,则有![]()
③当![]() 时,
时, ![]() 点与
点与![]() 点重合,这与已知条件矛盾,故此种情况不存在.
点重合,这与已知条件矛盾,故此种情况不存在.
试题解析:(1)由题意![]()
![]()
∵四边形ABCO为矩形,AB=16,
![]()
∴A点坐标为(12,0),
∵点D与点A关于y轴对称,
∴D(12,0).

(2)点D与点/span>A关于y轴对称,∴∠CDE=∠CAO,
∵∠CEF=∠ACB,∠ACB=∠CAO,
∴∠CDE=∠CEF,
又∵∠AEC=∠AEF+∠CEF=∠CDE+∠DCE(三角形外角性质)
∴∠AEF=∠DCE.
则在△AEF与△DCE中,∠CDE=∠CAO,∠AEF=∠DCE,
∴△AEF∽△DCE.
(3)当△EFC为等腰三角形时,有以下三种情况:
①当CE=EF时,
∵△AEF∽△DCE,
![]()
∴AE=CD=20,
∴OE=AEOA=2012=8,
∴E(8,0);
②当EF=FC时,如图②所示,过点F作FM⊥CE于M,则点M为CE中点,

![]()
∵△AEF∽△DCE,
![]() 即
即 解得
解得![]()
![]()
![]()
③当CE=CF时,则有∠CFE=∠CEF,
∵∠CEF=∠ACB=∠CAO,
∴∠CFE=∠CAO,即此时![]() 点与
点与![]() 点重合,这与已知条件矛盾.
点重合,这与已知条件矛盾.
综上所述,当△EFC为等腰三角形时,点E的坐标为(8,0)或![]()


科目:初中数学 来源: 题型:
【题目】中国最长铁路隧道西康铁路秦岭一线隧道全长十八点四六千米,为目前中国铁路隧道长度之首,被称为”神州第一长隧”.为了安全起见在某段隧道两旁安置了两座可旋转探照灯.如图1所示,灯A发出的光束从AC开始顺时针旋转至AD便立即回转,灯B发出的光束从BE开始顺时针旋转至BF便立即回转,两灯不停交叉照射巡视.若灯A旋转的速度是每秒3度,灯B旋转的速度是每秒2度.已知CD∥EF,且∠BAD=![]() ∠BAC,设灯A旋转的时间为t(单位:秒).
∠BAC,设灯A旋转的时间为t(单位:秒).
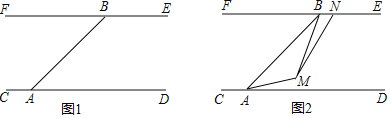
(1)求∠BAD的度数;
(2)若灯B发出的光束先旋转10秒,灯A发出的光束才开始旋转,在灯B发出的光束到达BF之前,若两灯发出的光束互相平行,求灯A旋转的时间t;
(3)如图2,若两灯同时转动,在灯A发出的光束到达AD之前,若两灯发出的光束交于点M,过点M作∠AMN交BE于点N,且∠AMN=135°.请探究:∠BAM与∠BMN的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是__(把你认为正确结论的序号都填上.)
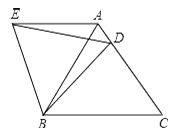
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两种型号台灯,若购买2台A型台灯和6台B型台灯共需610元.若购买6台A型台灯和2台B型台灯共需470元.
(1)求A、B两种型号台灯每台分别多少元?
(2)采购员小红想采购A、B两种型号台灯共30台,且总费用不超过2200元,则最多能采购B型台灯多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个边长为m+3的正方形,先将这个正方形两邻边长分别增加1和减少1,得到的长方形①的面积为S1.
(1)试探究该正方形的面积S与S1的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由;
(2)再将这个正方形两邻边长分别增加4和减少2,得到的长方形②的面积为S2.
①试比较S1,S2的大小;
②当m为正整数时,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有16个,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
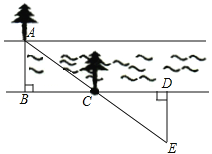
求:(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一副三角板的直角重合放置,其中∠A=30°,∠CDE=45°.
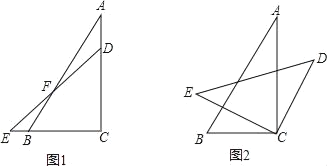
(1)如图1,求∠EFB的度数;
(2)若三角板ACB的位置保持不动,将三角板CDE绕其直角顶点C顺时针方向旋转.
①当旋转至如图2所示位置时,恰好CD∥AB,则∠ECB的度数为 ;
②若将三角板CDE继续绕点C旋转,直至回到图1位置.在这一过程中,是否还会存在△CDE其中一边与AB平行?如果存在,请你画出示意图,并直接写出相应的∠ECB的大小;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com