
����Ŀ��ij�κ�����������ƽ�еģ���ѧ��ȤС������ʦ�����²�����ˮ���ӾͲ�úӵĿ��ȣ��������������ģ�
���ں�����һ������B�㣬ѡ�����Ե�һ����A��
���غӰ�ֱ��20m��һ��C������ǰ��20m����D����
����D���غӰ���ֱ�ķ������ߣ�������A�����ñ�C���ڵ�ס��E��ֹͣ���ߣ�
�����DE�ij�Ϊ5�ף�
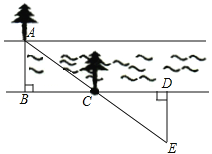
��1���ӵĿ����Ƕ����ף�
��2������֤��������������ȷ�ԣ�
���𰸡���1���ӵĿ�����5m����2��֤��������
��������
�����������1������ȫ�������ζ�Ӧ����ȿɵ�AB=DE��
��2���������DZ߽���֤��Rt��ABC��Rt��EDCȫ�ȣ��ٸ���ȫ�������ζ�Ӧ����Ƚ��
��1���⣺�ӵĿ�����5m��
��2��֤����������֪��BC=DC����ABC=��EDC=90����
��Rt��ABC��Rt��EDC��
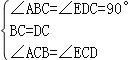 ��
��
��Rt��ABC��Rt��EDC��ASA����
��AB=ED��
�����ǵ���������ȷ�ģ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ������һ��������Ŀ��Ϊ�˽�Լ��Դ����������������ҵ��������A��B�����ͺŵ���ˮ�����豸��8̨������������±���
A�� | B�� | |
�۸���Ԫ/̨�� | 12 | 10 |
����ˮ������������/�£� | 200 | 160 |
��Ԥ�㣬��ҵ���֧��89��Ԫ�����豸����Ҫ���´�����ˮ����������1380�֣�
��1������ҵ�м��ֹ�����
��2�����ַ�����ʡǮ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԲOֱ��DE=12��Rt��ABC�У�BC=12����ACB=90������ABC=30������ԲO�������˶������˶������У���D��Eʼ����ֱ��BC�ϣ���ԲO����ABC����࣮
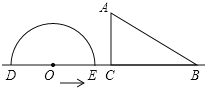
��1������ABC��һ�����ԲO����ʱ���뻭�����������ͼ�Σ�
��2������ABC��һ�����ԲO����ʱ�������ԲO��ֱ��DEΧ�ɵ���������ABC������Χ�ɵ��������ص����֣����ص����ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����Ϊ18cmϸ��Χ��һ�����������Σ�
��1����������ǵױߵ�2������ô���ߵij��Ƕ��٣�
��2����Χ����һ�ߵij�Ϊ4cm�ĵ�����������Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������O��BC���е���D��DE��AC��E������AD�������н��ۣ�
��AD��BC������EDA=��B����OA=![]() AC����DE����O�����ߣ���ȷ�ĸ����ǣ� ��
AC����DE����O�����ߣ���ȷ�ĸ����ǣ� ��
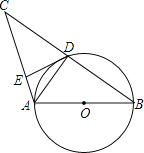
A��1 �� B��2�� C��3 �� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ��������ȫƽ����ʽ������ʽ�ֽ���ǣ�������
A. x2+x+1 B. x2+2x��1 C. x2��1 D. x2��6x+9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ACB=90������A=30����BD����ABC�Ľ�ƽ���ߣ�DE��AB�ڵ�E��
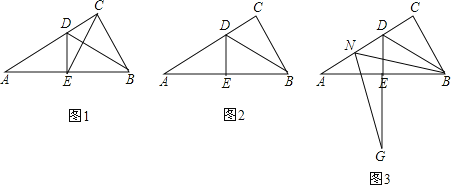
��1����ͼ1������EC����֤����EBC�ǵȱ������Σ�
��2����M���߶�CD�ϵ�һ�㣨�����C��D�غϣ�����BMΪһ�ߣ���BM���·�����BMG=60����MG��DE�ӳ����ڵ�G��������ͼ2�л�������ͼ�Σ���ֱ��д��MD��DG��AD֮���������ϵ��
��3����ͼ3����N���߶�AD�ϵ�һ�㣬��BNΪһ�ߣ���BN���·�����BNG=60����NG��DE�ӳ����ڵ�G����̽��ND��DG��AD����֮��Ĺ�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com