
【题目】如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧.
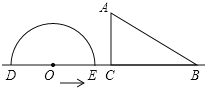
(1)当△ABC的一边与半圆O相切时,请画出符合题意得图形.
(2)当△ABC的一边与半圆O相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,求重叠部分的面积.
【答案】(1)见解析;(2)9π或9![]() +6π.
+6π.
【解析】
试题分析:(1)因为点D,E始终在直线BC,所以当△ABC的一边与半圆O相切时只有三种情况,再分别画出即可;
(2)本题要分当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形分别计算即可.
解:(1)如图所示:
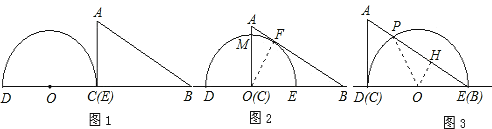
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形.
①如图2,设OA与半圆O的交点为M,易知重叠部分是圆心角为90°,半径为6cm的扇形,所求重叠部分面积为:S扇形EOM=![]() π×62=9π(cm2)
π×62=9π(cm2)
②如图3,设AB与半圆O的交点为P,连接OP,过点O作OH⊥AB,垂足为H.
则PH=BH.在Rt△OBH中,∠OBH=30°,OB=6cm
则OH=3cm,BH=3![]() cm,BP=6
cm,BP=6![]() cm,S△POB=
cm,S△POB=![]() ×6
×6![]() ×3=9
×3=9![]() (cm2)
(cm2)
又因为∠DOP=2∠DBP=60°
所以S扇形DOP=6π(cm2)
所求重叠部分面积为:S△POB+S扇形DOP=9![]() +6π(cm2),
+6π(cm2),
综上可知当半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分则重叠部分的面积是9π或9![]() +6π.
+6π.


科目:初中数学 来源: 题型:
【题目】在学习中,小明发现:当n=1,2,3时,n2—10n的值都是负数.于是小明猜想:当n为任意正整数时,n2-10n的值都是负数.判断小明的猜想是真命题还是假命题,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
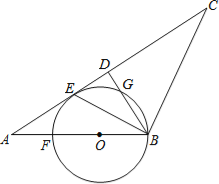
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本1.4有这样一道例题:
问题4:用一根长22cm的铁丝:
(1)能否围成面积是30cm2的矩形?
(2)能否围成面积是32cm2的矩形?
据此,一位同学提出问题:“用这根长22cm的铁丝能否围成面积最大的矩形?若能围成,求出面积最大值;若不能围成,请说明理由.”请你完成该同学提出的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
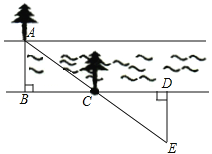
求:(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点A开始沿AC向点C以2厘米/秒的速度运动;与此同时,点Q从点C开始沿CB边向点B以1厘米/秒的速度运动;如果P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动.

(1)经过几秒,△CPQ的面积等于3cm2?
(2)在整个运动过程中,是否存在某一时刻t,使PQ恰好平分△ABC的面积?若存在,求出运动时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】森林是地球之肺,每年能为人类提供大约28.3亿吨的有机物.28.3亿吨用科学记数法表示为( )
A.28.3×107 B.2.83×108
C.0.283×1010 D.2.83×109
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com