
【题目】课本1.4有这样一道例题:
问题4:用一根长22cm的铁丝:
(1)能否围成面积是30cm2的矩形?
(2)能否围成面积是32cm2的矩形?
据此,一位同学提出问题:“用这根长22cm的铁丝能否围成面积最大的矩形?若能围成,求出面积最大值;若不能围成,请说明理由.”请你完成该同学提出的问题.
【答案】(1)能围成面积是30cm2的矩形,此时长和宽分别为5cm、6cm;(2)当矩形的各边长均为![]() cm时,围成的面积最大,最大面积是
cm时,围成的面积最大,最大面积是![]() cm2.
cm2.
【解析】
试题分析:(1)设当矩形的一边长为x cm时,由矩形的面积公式列出方程,解方程即可;(2)同(1)列出方程,由判别式<0,即可得出结果;
提出问题:设当矩形的一边长为x cm时,面积为y cm2.由矩形的面积公式和配方法得出得出y=﹣x2+11x=﹣(x﹣![]() )2+
)2+![]() ,由偶次方的性质,即可得出结果.
,由偶次方的性质,即可得出结果.
解:(1)设当矩形的一边长为x cm时,
根据题意得:x(11﹣x)=30,
整理得:x2﹣11x+30=0,
解得:x=5,或x=6,
当x=5时,11﹣x=6;
当x=6时,11﹣x=5;
即能围成面积是30cm2的矩形,此时长和宽分别为5cm、6cm;
(2)根据题意得:x(11﹣x)=32,
整理得:x2﹣11x+32=0,
∵△=(﹣11)2﹣4×1×32<0,
方程无解,因此不能围成面积是32cm2的矩形;
提出问题:能围成;理由如下:
设当矩形的一边长为x cm时,面积为y cm2.
由题意得:y=x(![]() ﹣x)=﹣x2+11x=﹣(x﹣
﹣x)=﹣x2+11x=﹣(x﹣![]() )2+
)2+![]() ,
,
∵(x﹣![]() )2≥0,
)2≥0,
∴﹣(x﹣![]() )2+
)2+![]() ≤
≤![]() .
.
∴当x=![]() 时,y有最大值=
时,y有最大值=![]() ,此时
,此时![]() ﹣x=
﹣x=![]() .
.
答:当矩形的各边长均为![]() cm时,围成的面积最大,最大面积是
cm时,围成的面积最大,最大面积是![]() cm2.
cm2.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】根据下列已知条件,能画出唯一△ABC的是( )
A. AB=3,BC=4,∠C=50° B. AB=4,BC=3,∠A=30°
C. ∠A=60°,∠B=45°,AB=4 D. ∠C=90°,AB=6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
月污水处理能力(吨/月) | 200 | 160 |
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=![]() DC.若AB=16,BC=20,则图中阴影部分的面积是 .
DC.若AB=16,BC=20,则图中阴影部分的面积是 .
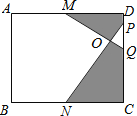
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧.
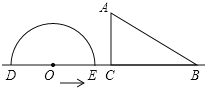
(1)当△ABC的一边与半圆O相切时,请画出符合题意得图形.
(2)当△ABC的一边与半圆O相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
①AD⊥BC;②∠EDA=∠B;③OA=![]() AC;④DE是⊙O的切线,正确的个数是( )
AC;④DE是⊙O的切线,正确的个数是( )
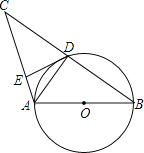
A.1 个 B.2个 C.3 个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2,我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.

【问题探究】
(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为 .
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.
【问题拓展】
(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G,将∠AEG绕点A顺时针旋转30°,得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′C′,分别在直线l2,l4上,求菱形AB′C′D′的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com