
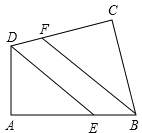
【题目】如图,四边形ABCD中,∠A=∠C=90°,BF、DE分别平分∠ABC、∠ADC.判断DE、BF是否平行,并说明理由.
【答案】ED∥BF;证明见解析.
【解析】
试题分析:由题意可知∠ADC+∠ABC=180°,由BF、DE分别平分∠ABC、∠ADC可知:∠ADE+∠ABF=90°,又因为∠ADE+∠AED=90°,所以可得∠AED=∠ABF,即可得ED∥BF.
试题解析:ED∥BF;证明如下:
∵四边形ABCD中,∠A=∠C=90°,
∴∠ADC+∠ABC=180°,
∵BF、DE分别平分∠ABC、∠ADC,
∴∠ADC+∠ABC=2∠ADE+2∠ABF=180°,
∴∠ADE+∠ABF=90°,
又∵∠A=90°,∠ADE+∠AED=90°,
∴∠AED=∠ABF,
∴ED∥BF(同位角相等,两直线平行).


科目:初中数学 来源: 题型:
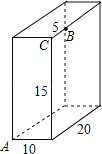
【题目】如图,长方体的长为15cm,宽为10cm,高为20cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
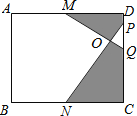
【题目】如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=![]() DC.若AB=16,BC=20,则图中阴影部分的面积是 .
DC.若AB=16,BC=20,则图中阴影部分的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
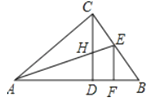
【题目】如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,下列结论:①∠ACD=∠B;②CH=CE=EF;③AC=AF;④CH=HD.其中正确的结论为( )
A.①②④ B.①②③ C.②③ D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧.
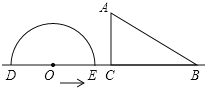
(1)当△ABC的一边与半圆O相切时,请画出符合题意得图形.
(2)当△ABC的一边与半圆O相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点A、C同时出发,运动速度均为1cm/s,点P从点A出发,沿A→B运动,到点B停止,点Q从点C出发,沿C→A运动,到点A停止,连接BQ、CP相交于点D,设点P的运动时间为x(s).
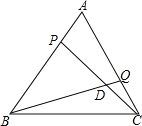
(1)AP= (用含x的式子表示);
(2)求证:△ACP≌△CBQ;
(3)求∠PDB的度数;
(4)当CP⊥AB时,直接写出x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com