
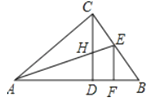
【题目】如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,下列结论:①∠ACD=∠B;②CH=CE=EF;③AC=AF;④CH=HD.其中正确的结论为( )
A.①②④ B.①②③ C.②③ D.①③
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 四个数2、3、5、4的中位数为4
B. 了解重庆初三学生备战中考复习情况,应采用普查
C. 小明共投篮25次,进了10个球,则小明进球的频率是0.4
D. 从初三体考成绩中抽取100名考生的体考成绩,这100名考生是总体的一个样本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长都为整数的△ABC≌△DEF,AB与DE是对应边,AB=2,BC=4.若△DEF的周长为偶数,则DF的长为( )
A. 3 B. 4 C. 5 D. 3或4或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
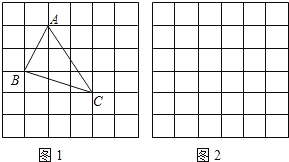
(1)请你将△ABC的面积直接填写在横线上.
(2)画△DEF,DE、EF、DF三边的长分别为![]() 、
、![]() 、
、![]()
①判断三角形的形状,说明理由.
②求这个三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com